阅读量： 26

最近更新于 2025-08-16 23:41

图像

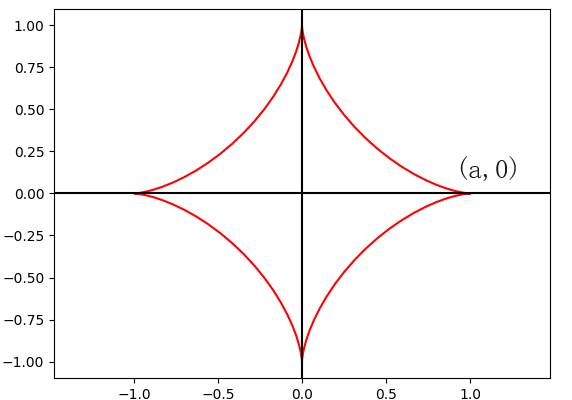
使用下面的 Python 代码绘制，a 取值 1 时
(本文代码都是在 Jupyter 环境下运行测试的)

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)
x = alpha * np.cos(theta)**3
y = alpha * np.sin(theta)**3

plt.axis('equal')
plt.plot(x, y, color='r')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')

方程

 $\begin{array}{l} 极坐标方程：\rho=\frac{1}{(\cos^\frac{2}{3}\theta+\sin^\frac{2}{3})^\frac{3}{2}}（a>0，\theta\in[0,2\pi]）\\ \\ 直角坐标系方程：x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}（a\gt0），可表示为\ y=(a^\frac{2}{3} - x^\frac{2}{3})^\frac{3}{2}\\ \\ 参数方程：\begin{cases} x = a\cos^3\theta \\ y = a\sin^3\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

平面周长计算

方法一：直角坐标方程

弧微分参考：https://blog.iyatt.com/?p=10934

 $\begin{array}{l} y'=\frac{3}{2}(a^\frac{2}{3} - x^\frac{2}{3})^\frac{1}{2}(-\frac{2}{3}x^{-\frac{1}{3}})=-(a^\frac{2}{3} - x^\frac{2}{3})^\frac{1}{2}x^{-\frac{1}{3}} \\ \\ \begin{aligned} L&=4\int_0^a\sqrt{1+y'^2}dx \\ &=4\int_0^a\sqrt{1+(a^\frac{2}{3} - x^\frac{2}{3})x^{-\frac{2}{3}}}dx \\ &=4\int_0^a|a^\frac{1}{3}x^{-\frac{1}{3}}|dx \\ &=4\times a^\frac{1}{3}\times\frac{3}{2}x^\frac{2}{3}|_0^a \\ &=6a \end{aligned} \end{array}$

方法二：参数方程

 $\begin{aligned} L&=4\times\int_0^{\frac{\pi}2}\sqrt{x'^2(\theta)+y'^2(\theta))}d\theta\\ &=4\times\int_0^{\frac{\pi}2}\sqrt{[3a\cos^2\theta(-\sin \theta)]^2+(3a\sin^2\theta\cos \theta)^2}\ d\theta\\ &=4\times\int_0^{\frac{\pi}2}\sqrt{9a^2\sin^2\theta\cos^2\theta(\sin^2\theta+\cos^2\theta)}d\theta\\ &=4\times\int_0^{\frac{\pi}2}3a\sin\theta\cos\theta d\theta\\ &=12a\times\int_0^{\frac{\pi}2}\sin\theta d\sin\theta\\ &=6a\times sin^2\theta|_0^{\frac{\pi}2}\\\\ &=6a \end{aligned}$

平面面积计算

计算中用到的 Wallis 公式参考：https://blog.iyatt.com/?p=11779

方法一：直角坐标方程

 $\begin{aligned} A&=4\int_0^aydx \\ &=4\int_0^a(a^\frac{2}{3}-x^\frac{2}{3})^\frac{3}{2} \\ &\xlongequal{x=a\sin^3\theta}12a\int_0^\frac{\pi}{2}(a^\frac{2}{3}-a^\frac{2}{3}\sin^2\theta)^\frac{3}{2}\sin^2\theta\cos\theta d\theta \\ &=12a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta d\theta \\ &=12a^2\int_0^\frac{\pi}{2}\cos^4\theta(1-\cos^2\theta)d\theta \\ &=12a^2(\int_0^\frac{\pi}{2}\cos^4\theta d\theta-\int_0^\frac{\pi}{2}\cos^6\theta d\theta) \\ &=12a^2(\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}-\frac{5}{6}\times\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}) \\ &=\frac{3}{8}\pi a^2 \end{aligned}$

方法二：参数方程

 $\begin{aligned} A&=4\int_0^aydx \\ &=4\int_{\frac{\pi}2}^0a\sin^3\theta\cdot3a\cos^2\theta(-\sin\theta)d\theta\\ &=12a^2\int_0^{\frac{\pi}2}\sin^4\theta\cos^2\theta d\theta\\ &=12a^2\int_0^{\frac{\pi}2}\sin^4\theta(1-\sin^2\theta)d\theta\\ &=12a^2\int_0^{\frac{\pi}2}(\sin^4\theta-\sin^6\theta)d\theta\\ &=12a^2(\frac{3}{4}\times\frac12\times\frac{\pi}2-\frac56\times\frac{3}{4}\times\frac12\times\frac{\pi}2)\\ &=\frac{3\pi a^2}8 \end{aligned}$

旋转体

旋转动画

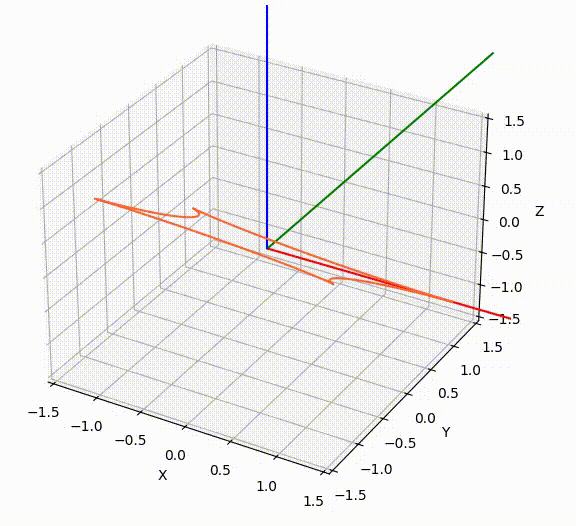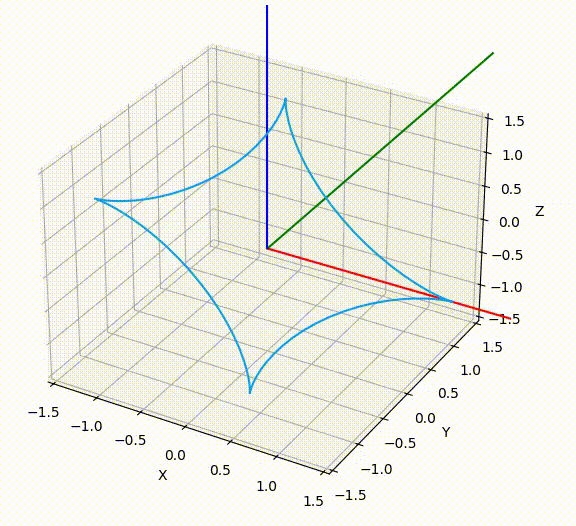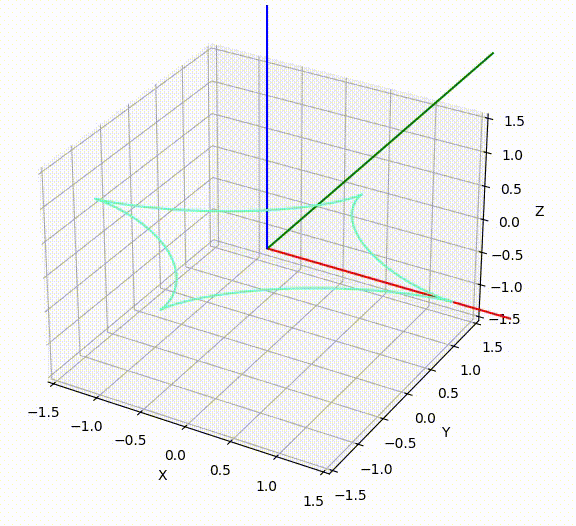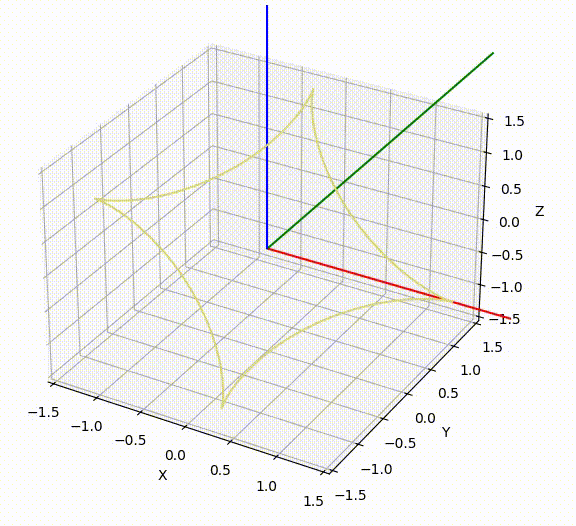
旋转动画由下面 Python 代码生成

%matplotlib widget
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib.animation import FuncAnimation

alpha = 2

# 星形线参数方程
def star(t):
    x = alpha * np.cos(t)**3
    y = alpha * np.sin(t)**3
    return x, y

# 创建一个三维坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

t = np.linspace(0, 2 * np.pi, 100)
x, y = star(t)

cmap = plt.get_cmap('rainbow')

# 定义初始化函数，清空当前帧
def init():
    ax.clear()
    return ax,

# 定义更新函数，绘制每一帧的图形
def update(frame):
    # 清空当前帧
    ax.clear()
    # 设置坐标轴的标签和范围
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_xlim(-1.5, 1.5)
    ax.set_ylim(-1.5, 1.5)
    ax.set_zlim(-1.5, 1.5)
    # 绘制三个坐标轴
    ax.plot([0, 5], [0, 0], [0, 0], color='r', label='X')
    ax.plot([0, 0], [0, 5], [0, 0], color='g', label='Y')
    ax.plot([0, 0], [0, 0], [0, 5], color='b', label='Z')
    # 计算旋转后的y和z坐标
    y_rot = y * np.cos(frame)
    z_rot = y * np.sin(frame)
    # 绘制旋转后的曲线
    ax.plot(x, y_rot, zs=z_rot, zdir='z', color=cmap(frame / (2*np.pi)))

# 创建动画对象，设置帧数，间隔和重复播放
ani = FuncAnimation(fig, update, frames=np.linspace(0, 2 * np.pi, 100), init_func=init, interval=10, repeat=True)

旋转体图像

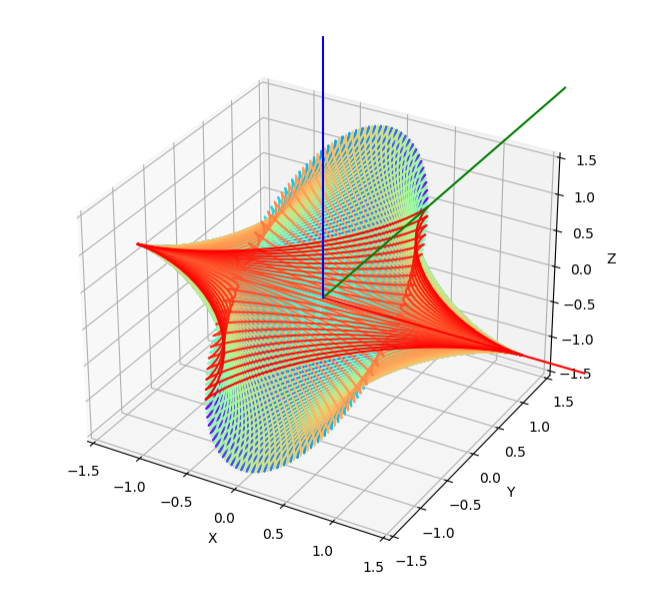
旋转体图像由下面 Python 代码生成

%matplotlib widget
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

alpha = 2

# 星形线参数方程
def star(t):
    x = alpha * np.cos(t)**3
    y = alpha * np.sin(t)**3
    return x, y

# 创建一个三维坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

t = np.linspace(0, 2 * np.pi, 100)
x, y = star(t)

cmap = plt.get_cmap('rainbow')

# 将星形线以 x 轴为中心线旋转一周，得到三维图形
for angle in np.linspace(0, 2 * np.pi, 100):
    # 计算旋转后的 y 和 z 坐标
    y_rot = y * np.cos(angle)
    z_rot = y * np.sin(angle)
    ax.plot(x, y_rot, zs=z_rot, zdir='z', color=cmap(angle / (2*np.pi)))

# 设置坐标轴的标签和范围
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)

ax.plot([0, 5], [0, 0], [0, 0], color='r', label='X')
ax.plot([0, 0], [0, 5], [0, 0], color='g', label='Y')
ax.plot([0, 0], [0, 0], [0, 5], color='b', label='Z')

旋转体体积计算

星形线旋转体体积计算可以看作是圆柱的体积计算，就是底面积乘以高。
y 轴左右两部分的体积相等，那么可以只计算右侧的。
底面圆半径就是 y，底面积就是 $\pi y^2$ ，高是对弧微分进行 0 到 a 的积分（y 轴右半部分），再乘以 2 就是要计算的体积。

方法一：直角坐标方程

 $\begin{array}{l} y^2=(a^\frac{2}{3} - x^\frac{2}{3})^3 \\ \begin{aligned} V&=2\pi\int_0^ay^2dx \\ &=2\pi\int_0^a(a^\frac{2}{3} - x^\frac{2}{3})^3dx \\ &\xlongequal{x=a\sin^3\theta}2\pi\int_0^a(a^\frac{2}{3}-a^\frac{2}{3}\sin^2\theta)^3\cdot3a\sin^2\theta\cos\theta d\theta \\ &=6\pi a^3\int_0^a\cos^7\theta\sin^2\theta d\theta \\ &=6\pi a^3\int_0^a\cos^7\theta(1-\cos^2\theta)d\theta \\ &=6\pi a^3\int_0^a(\cos^7\theta-\cos^9\theta)d\theta \\ &\xlongequal{Wallis公式}6\pi a^3(\frac{6\times4\times2}{7\times5\times3}-\frac{8\times6\times4\times2}{9\times7\times5\times3}) \\ &=\frac{32}{105}\pi a^3 \end{aligned} \end{array}$

方法二：参数方程

 $\begin{aligned} V&=2\pi\int_0^ay^2dx\\ &=2\pi\int_{\frac{\pi}2}^0a^2\sin^6\theta\cdot3a\cos^2\theta(-\sin\theta)d\theta\\ &=6\pi a^3\int_0^{\frac{\pi}2}\sin^7\theta\cos^2\theta d\theta\\ &=6\pi a^3\int_0^{\frac{\pi}2}\sin^7\theta(1-\sin^2\theta)d\theta\\ &=6\pi a^3\int_0^{\frac{\pi}2}(\sin^7\theta-\sin^9\theta)d\theta\\ &=6\pi a^3(\frac67\times\frac45\times\frac23-\frac89\times\frac67\times\frac45\times\frac23)\\ &=\frac{32}{105}\pi a^3 \end{aligned}$

旋转体侧面积计算

星形线旋转体侧面积计算可以看作是圆柱的侧面积计算，就是底面圆周长乘以高。
底面圆半径就是 y，底面周长就是 $2\pi y$ ，高是对弧微分进行 0 到 a 的积分（y 轴右半部分），积分结果就是右半部分，再乘以 2 就是要计算的侧面积。

方法一：直角坐标方程

 $\begin{aligned} S&=2\times2\pi\int_0^ay\sqrt{1+y'^2}dx \\ &=4\pi\int_0^a|(a^\frac{2}{3} - x^\frac{2}{3})^\frac{3}{2}|\sqrt{1+(a^\frac{2}{3} - x^\frac{2}{3})x^{-\frac{2}{3}}}dx \\ &\xlongequal{x=a\sin^3\theta}4\pi\int_0^\frac{\pi}{2}|a\cos^3\theta|\sqrt{1+\cos^2\theta\sin^{-2}\theta}\times3a\sin^2\theta\cos\theta d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta\sqrt{1+\cot^2\theta}d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta|\csc\theta|d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta|\sin\theta|d\theta \\ &=-12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta d\cos\theta \\ &=-12\pi a^2\cdot\frac{1}{5}\cos^5\theta|_0^\frac{\pi}{2} \\ &=\frac{12}{5}\pi a^2 \end{aligned}$

方法二：参数方程

 $\begin{aligned} S&=2\times2\pi\int_0^{\frac\pi2}y(t)\sqrt{[x'^2(t)]+[y'^2(t)]}\ dt\\ &=4\pi\int_0^\frac\pi2a\sin^3t\sqrt{[3a\cos^2t(-\sin t)]^2+(3a\sin^2t\cos t)^2}dt\\ &=4\pi\int_0^\frac\pi2a\sin^3t\sqrt{9a^2\sin^2t\cos^2t(\sin^2t+\cos^2t)}\\ &=12\pi a^2\int_0^\frac\pi2\sin^4t\cos tdt\\ &=12\pi a^2\int_0^\frac\pi2\sin^4td\sin t\\ &=12\pi a^2\times\frac15\sin^5t|_0^\frac\pi2\\ &=\frac{12}5\pi a^2 \end{aligned}$

星形线