阅读量： 67

最近更新于 2023-09-30 20:00

函数的单调性

设f(x)在[a,b]内连续，在(a,b)内可导。
①若在(a,b)内， $f'(x)\gt0$ ，则f(x)在[a,b]单调递增；
②若在(a,b)内， $f'(x)\lt0$ ，则f(x)在[a,b]单调递减；

函数的极值

设y=f(x)在 $U(x_0,\delta)$ 有定义。如果对于该邻域内任何x，恒有 $f(x)\le f(x_0)$ 或 $f(x)\ge f(x_0)$ ，则称 $x_0$ 为f(x)的一个极大值点或极小值点，称 $f(x_0)$ 为极大值或极小值，都统称为极值，对应的点统称为极值点。导数为0的点称为函数的驻点。

极值的必然条件

设y=f(x)在点 $x_0$ 处可导，如果 $x_0$ 为f(x)的极值点，则 $f'(x_0)=0$ 。

极值的第一充分条件

f(x)在 $\mathring{U}(x_0,\delta)$ 内可导，且 $f'(x_0)=0$ 或 $f'(x_0)$ 不存在但是f(x)在 $x_0$ 处连续（比如f(x)=|x|在x=0处导数不存在，但是连续）。
若 $x\lt x_0$ 时， $f'(x)\ge0$ ； $x>x_0$ 时， $f'(x)\le0$ ，则f(x)在 $x_0$ 处取极大值；
若 $x\lt x_0$ 时， $f'(x)\le0$ ； $x>x_0$ 时， $f'(x)\ge0$ ，则f(x)在 $x_0$ 处取极大值；
若f(x)在 $x_0$ 两侧不变号，则 $x_0$ 不是f(x)的极值点。

极值的第二充分条件

$f'(x_0)=0，f''(x_0)\ne0$ 时，
$f''(x_0)<0$ ，在 $x_0$ 处为极大值点；
$f''(x_0)>0$ ，在 $x_0$ 处为极小值点；
$f''(x_0)=0$ ，不能判定 $x_0$ 是否为极值点。

函数的最大值和最小值

设函数y=f(x)在[a,b]有定义， $x_0\in[a,b]$ ，若对于 $\forall x\in[a,b]$ ，恒有 $f(x)\le f(x_0)$ 或 $f(x)\ge f(x_0)$ ，则称 $f(x_0)为函数$ f(x)在[a,b]上的最大值或最小值，称 $x_0$ 为f(x)在[a,b]上的最大值点或最小值点。

曲线的凹凸性

设函数f(x)在区间I上连续，如果对I上任意两点 $x_1,x_2$ ，恒有

 $f(\frac{x_1+x_2}{2})\lt\frac{f(x_1)+f(x_2)}{2}$

则称f(x)在I上的图形是凹的，如果恒有

 $f(\frac{x_1+x_2}{2})\gt\frac{f(x_1)+f(x_2)}{2}$

则称f(x)在I上的图形是凸的。

凹凸判定

设函数y=f(x)在[a,b]上连续，在(a,b)内二阶可导
若在(a,b)内有 $f''(x)\gt0$ ，则f(x)在[a,b]内图形是凹的；
若在(a,b)内有 $f''(x)\lt0$ ，则f(x)在[a,b]内图形是凸的。

拐点

连续曲线弧上的凹与凸的分界点称为曲线弧的拐点。

必要条件

设y=f(x)在点 $x_0$ 处二阶可导，且点 $(x_0,f(x_0))$ 为曲线y=f(x)的拐点，则 $f''(x_0)=0$ 。

第一充分条件

设y=f(x)在 $\mathring{U}(x_0,\delta)$ 二阶可导，且 $f''(x_0)=0$ （或f(x)在 $x_0$ 处连续）。
若 $f''(x_0)$ 在 $x_0$ 左右两侧异号，则点 $(x_0,f(x_0))$ 是曲线y=f(x)的拐点；
若 $f''(x_0)$ 在 $x_0$ 左右两侧同号，则点 $(x_0,f(x_0))$ 不是曲线y=f(x)的拐点；

第二充分条件

设y=f(x)在 $x_0$ 处三阶可导，且 $f''(x_0)=0$ 。

若 $f'''(x_0)\ne0$ ，则点 $(x_0, f(x_0))$ 是曲线y=f(x)的拐点；
若 $f'''(x_0)=0$ ，则该方法不能判断拐点。

曲线的渐近线

弱点M沿曲线y=f(x)无限远离远点时，它与某条定直线L之间的距离将趋近于零，则称直线L为曲线y=f(x)的一条渐近线。若直线L与x轴平行，则称L为曲线y=f(X)的水平渐近线；若直线L与x轴垂直，则称L为曲线y=f(x)的铅直渐近线；排除这两种情况，就属于斜渐近线。

水平渐近线

$\lim_{x\to\infty}f(x)=A$ ，y=A就是y=f(x)的水平渐近线。

铅直渐近线

$\lim_{x\to x_0}f(x)=\infty$ ， $x=x_0$ 就是y=f(x)铅直渐近线

斜渐近线

若 $\lim_{x\to\infty}\frac{f(x)}{x}=a$ （a为非零常数），且 $\lim_{x\to\infty}[f(x)-ax]=b$ ，那么y=ax+b就是y=f(x)的斜渐近线。

曲线和弧微分和曲率

设y=f(x)在(a,b)内有连续导数，则有弧微分： $ds=\sqrt{1+y'^2}dx$
设y=f(x)有二阶导数，则有曲率： $K=\frac{|y''|}{(1+y'^2)^{\frac{3}{2}}}$
称 $\rho=\frac{1}{K}$ 为曲率半径。

若曲线y=f(x)在点M(x,y)处的曲率为 $K（K\ne0）$ 。在点M处曲线的法线上，在曲线凹的一侧取一点D，使 $|DM|=\frac{1}{K}=\rho$ ，以D为圆心， $\rho$ 为半径的圆称为曲线在点M处的曲率圆，圆心D称为曲线在点M处的曲率中心。

推导与理解

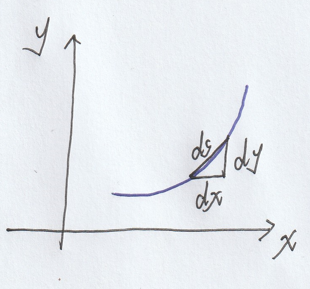
在一段弧上取一段小弧，这段小弧足够小，即dx足够小，那么这段小弧的长度就可以近似看作小弧两端点直线连接的距离，对应 $ds=\sqrt{(dx)^2+(dy)^2}=\sqrt{(dx)^2+(y'\cdot dx)^2}=\sqrt{1+y'^2}dx$ ，这就是弧微分。

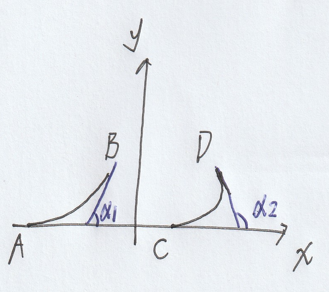
弧 AB 和弧 CD 长度相等，弧 AB 从 A 点起始到 B 点结束，切线旋转的角度就是 $\alpha_1$ ，弧 CD 切线旋转的角度为 $\alpha_2$ ，从相同弧长切线旋转的角度就能体现出这个弧的弯曲程度。那么这就可以引出曲率的定义，也就是单位弧长切线方向角的转动大小。有

 $\begin{array}{l} y'=\frac{dy}{dx}，几何意义上反映曲线上某点的切线斜率，那么可以表示为 y'=\tan\theta，\theta 为该点的切线与 x 轴的夹角。 \\ \theta=\arctan y' \\ d\theta=\frac{y''}{1+y'^2}dx \\ 则曲率 K=|\frac{d\theta}{ds}|=\frac{|y''|}{(1+y'^2)^{\frac{3}{2}}} \end{array}$

曲率圆是反映了某点处最接近的近似圆，其半径为曲率的倒数，曲率半径越小曲线越接近圆，越大越接近直线。

导数的应用

作者IYATT-yx