最近更新于 2025-08-23 22:18

概念

逆序

设 i、j 是一对不等的正整数，若 i > j，则称 (i, j) 为一对逆序。

逆序数

例：求 421635 的逆序数，即 \tau(421635)
①4>2、4>1、4>3 有 3 个逆序
②2>1 有 1 个逆序
③1 不大于它右侧的任何数，有 0 个逆序
④6>3、6>5 有 2 个逆序
⑤3 不大于它右侧的 5，有 0 个逆序
则\tau(421635)=3+1+0+2+0=6

行列式

n\times n个数组成的方阵

D=
\left |
\begin{matrix}
a_{11}&a_{12}&\cdots&a_{1n} \\
a_{21}&a_{22}&\cdots&a_{2n} \\
\vdots&\vdots&\vdots&\vdots \\
a_{n1}&a_{n2}&\cdots&a_{nn} \\
\end{matrix}
\right |

余子式

a_{ij}的余子式表示为M_{ij}，由原矩阵去除第 i 行和第 j 列后剩余部分组成的新的行列式。
a_{ij}的代数余子式表示为A_{ij}，A_{ij}=(-1)^{i+j}M_{ij}

行列式计算

二阶行列式通用计算方法

\left |
\begin{array}{l}
a_{11}&a_{12}\\
a_{21}&a_{22}
\end{array}
\right |=
a_{11}a_{22}-a_{12}a_{21}

三阶行列式通用计算方法

\left |
\begin{array}{l}
a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}
\end{array}
\right |=
a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}

之积+

之积+

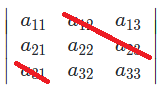
之积-

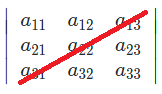
之积-

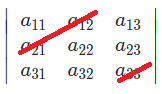
之积-

对角、上（下）三角行列式计算方法

主对角线

\left |
\begin{array}{l}
a_{11}&0&0&0\\
0&a_{22}&0&0\\
\vdots&\vdots&&\vdots\\
0&0&\cdots&a_{nn}
\end{array}
\right|
=
\left |
\begin{array}{l}
a_{11}&a_{12}&a_{13}&a_{14}\\
0&a_{22}&a_{23}&a_{24}\\
\vdots&\vdots&&\vdots\\
0&0&\cdots&a_{nn}
\end{array}
\right|
=
\left |
\begin{array}{l}
a_{11}&0&0&0\\
a_{21}&a_{22}&0&0\\
\vdots&\vdots&&\vdots\\
a_{n1}&a_{n2}&\cdots&a_{nn}
\end{array}
\right|
=
a_{11}a_{22}\cdots a_{nn}

副对角线

\left |
\begin{array}{l}
0&\cdots&0&l_1\\
0&\cdots&l_2&0\\
\vdots&&\vdots&\vdots\\
l_n&\cdots&0&0
\end{array}
\right|
=
\left |
\begin{array}{l}
0&\cdots&0&l_1\\
0&\cdots&l_2&a_j\\
\vdots&&\vdots&\vdots\\
l_n&\cdots&a_m&a_k
\end{array}
\right|
=
\left |
\begin{array}{l}
a_j&\cdots&a_m&l_1\\
a_k&\cdots&l_2&0\\
\vdots&&\vdots&\vdots\\
l_n&\cdots&0&0
\end{array}
\right|
=
(-1)^\frac{n(n-1)}{2}l_1l_2\cdots k_n

范德蒙行列式计算

V(a_1,a_2,\cdots,a_n)=
\left |
\begin{array}{l}
1&1&\cdots&1\\
a_1&a_2&\cdots&a_n\\
\vdots&\vdots&&\vdots\\
a_1^{n-1}&a_2^{n-2}&\cdots&a_n^{n-1}
\end{array}
\right |=
\prod_{1\le j\lt i\le n}(a_i-a_j)

例:

\begin{aligned}
\begin{vmatrix}
1&1&1\\
2&1&-3\\
4&1&9
\end{vmatrix}&=

\begin{vmatrix}
1&1&1\\
2^1&1^1&(-3)^1\\
2^2&1^2&(-3)^2
\end{vmatrix}\\
&=
(1-2)(-3-2)(-3-1)\\
&=
-20

\end{aligned}

分块行列式

\begin{array}{l}
\begin{vmatrix}
A_1&&&\\
&A_2&&\\
&&\ddots&\\
&&&A_n
\end{vmatrix}=
|A_1|\cdot|A_2|\cdot\cdots\cdot|A_n|\\ \\
\begin{vmatrix}
A&C\\
O&B
\end{vmatrix}
=
\begin{vmatrix}
A&O\\
D&B
\end{vmatrix}
=|A|\cdot|B|\\ \\

设 A，B 分别为 m，n 阶矩阵，则
\begin{vmatrix}
O&A\\
B&O
\end{vmatrix}
=
(-1)^{mn}|A|\cdot|B|
\end{array}

行列式变换性质

1.行列式 D 与其转置行列式 D^T相等。即 D=D^T；
2.行列式任意两行（或列）对换，改变符号。如\begin{vmatrix}a_1&a_2\\a_3&a_4\end{vmatrix}=-\begin{vmatrix}a_2&a_1\\a_4&a_3\end{vmatrix}
3.行列式某行（或列）有公因子，可以提取到行列式外面。如\begin{vmatrix}5a_1&5a_2\\a_3&a_4\end{vmatrix}=5\begin{vmatrix}a_1&a_2\\a_3&a_4\end{vmatrix}
3.1行列式某行（或列）元素全为0，则该行列式为0。r如\begin{vmatrix}a_1&a_2\\0&0\end{vmatrix}=0
3.2行列式某两行（或列）元素想同，则该行列式为0。如\begin{vmatrix}a_1&a_2\\a_1&a_2\end{vmatrix}=0
3.3行列式某两行（或列）元素对应成比例，则行列式为0。\begin{vmatrix}5a_1&5a_2\\a_1&a_2\end{vmatrix}=0
4.行列式某行（或列）的每个元素都是两数之和，行列式可分解为两个行列式之和。即\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\ a_{i1}+b_{i1}&a_{i2}+b_{i2}&\cdots&a_{in}+b_{in}\\ \vdots&\vdots&& \vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\ a_{i1}&a_{i2}&\cdots&a_{in}\\ \vdots&\vdots&& \vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}+\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\ b_{i1}&b_{i2}&\cdots&b_{in}\\ \vdots&\vdots&& \vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}
5.行列式的某行（或列）的任意倍数加到另外一行（或列），行列式值不变。如\begin{vmatrix}a_1&a_2\\a_3&a_4\end{vmatrix}=\begin{vmatrix}a_1&a_2\\a_3+3a_1&a_4+3a_2\end{vmatrix}

行列式降阶性质

1.行列式等于行列式某行（或列）元素与其对应的代数余子式之积的和，即D=a_{i1}A_{i1}+a_{i2}A_{i2}+\cdots+a_{in}A_{in}（i=1,2,\cdots,n）或D=a_{1j}A_{1j}+a_{2j}A_{2j}+\cdots+a_{nj}A_{nj}（j=1,2,\cdots,n）。如\begin{vmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\end{vmatrix}=1\times(-1)^{1+1}\begin{vmatrix}6&7&8\\10&11&12\\14&15&16\end{vmatrix}+2\times(-1)^{1+2}\begin{vmatrix}5&7&8\\9&11&12\\13&15&16\end{vmatrix}+3\times(-1)^{1+3}\begin{vmatrix}5&6&8\\9&10&12\\13&14&16\end{vmatrix}+4\times(-1)^{1+4}\begin{vmatrix}5&6&7\\9&10&11\\13&14&15\end{vmatrix}
2.行列式某行（或列）的元素与另外一行（或列）对应元素的代数余子式之积的和为0，即a_{i1}A_{j1}+a_{i2}A_{j2}+\cdots+a_{in}A_{jn}=0（i\ne j）或a_{1i}A_{1j}+a_{2i}A_{2j}+\cdots+a_{ni}A_{nj}=0（i\ne j）

a