不等式

最近更新于 2024-05-08 15:10

均值不等式

调和平均数 \frac{2}{\frac{1}{a}+\frac{1}{b}}
几何平均数 \sqrt{ab}
算数平均数 \frac{a+b}{2}
平方平均数 \sqrt{\frac{a^2+b^2}{2}}

关系

\frac{2}{\frac{1}{a}+\frac{1}{b}}\le\sqrt{ab}\le\frac{a+b}{2}\le\sqrt{\frac{a^2+b^2}{2}}，a=b时，等号成立

证明

几何

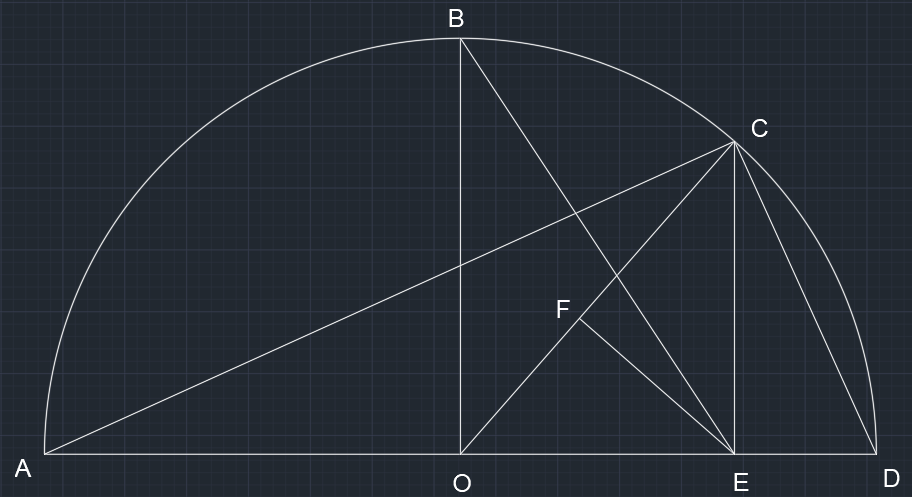
其中 BO\bot AD，CE\bot AD，EF\bot CO

设 AE = a，DE = b
算数均值 AO=DO=BO=CO=\frac{a+b}{2}（半径）
几何均值 CE=\sqrt{AE\cdot DE}=\sqrt{ab}(射影定理)
平方均值 BE=\sqrt{BO^2+EO^2}=\sqrt{\frac{a+b}{2}^2+(a-\frac{a+b}{2})^2}=\sqrt{\frac{a^2+b^2}{2}}
调和均值 CF=\frac{CE^2}{CO}=\frac{ab}{\frac{a+b}{2}}=\frac{1}{\frac{1}{a}+\frac{1}{b}}(射影定理)

BE\ge AO\ge CE\ge CF

注：
射影定理

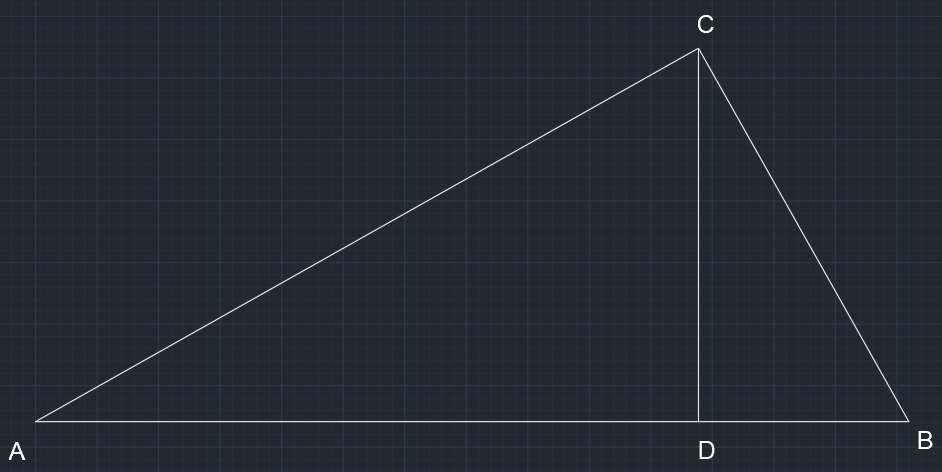
其中 AC\bot BC，CD\bot AB，有
CD^2=AD\cdot BD
AC^2=AB\cdot AD
BC^2=AB\cdot BD
AC\cdot BC=AB\cdot CD

数学

(a-b)^2\ge0 \\
a^2+b^2\ge2ab \\
\frac{a^2+b^2}{4}\ge\frac{2ab}{4} \\
\frac{2a^2+2b^2}{4}\ge\frac{a^2+b^2+2ab}{4}=\frac{(a+b)^2}{4} \\
\sqrt{\frac{a^2+b^2}{2}}\ge\frac{a+b}{2} \\
\ \\
(a-b)^2\ge0 \\
a^2+b^2\ge2ab \\
a^2+b^2+2ab\ge4ab \\
\frac{(a+b)^2}{4}\ge ab \\
\frac{a+b}{2}\ge\sqrt{ab} \\
\ \\
(a-b)^2\ge0 \\
a^2+b^2\ge2ab \\
a^2+b^2+2ab\ge4ab \\
ab(a^2+b^2+2ab)\ge4(ab)^2 \\
ab\ge\frac{4}{\frac{(a+b)^2}{(ab)^2}} \\
\sqrt{ab}\ge\frac{2}{\frac{a+b}{ab}}=\frac{2}{\frac{1}{a}+\frac{1}{b}}

绝对值三角不等式

||a|-|b||\le|a\pm b|\le|a|+|b|

ab\le0时，||a|-|b||\le|a+b|和|a-b|\le|a|+|b|等号成立
ab\ge0时，||a|-|b||\le|a-b|和|a+b|\le|a|+|b|等号成立

柯西不等式

(a_1b_1+a_2b_2+...+a_nb_n)^2\le(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)，\frac{a_1}{b_1}=\frac{a_2}{b_2}=\cdots=\frac{a_n}{b_n}时，等号成立