阅读量： 41

最近更新于 2024-03-29 22:28

1 随机事件

随机事件满足的特征：

可以在想用条件下重复执行
事先可知可能出现的结果
试验开始前不确定当次的结果

随机试验中每一个可能出现的试验结果称为一个样本点，记作 $\omega$ ，所有可能出现的试验结果组成的集合称为样本空间，记为 $\Omega$ ，即 $\Omega=\{\omega_1,\omega_2,\cdots,\omega_n\}$

1.1 事件间的关系与运算

 $\begin{array}{|l|l|l|} \hline 记号 & 概率论 & 集合论 \\ \hline \Omega & 样本空间，必然事件 & 全集 \\ \hline \emptyset & 不可能事件 & 空集 \\ \hline \omega & 基本事件 & 元素 \\ \hline A & 事件 & 子集 \\ \hline \overline{A} & 事件A的对立事件 & A的余集 \\ \hline A\subset B & 事件A发生导致事件B发生 & A是B的子集 \\ \hline A=B & 事件A与事件B相等 & A与B相等 \\ \hline A\cup B & 事件A与事件B至少有一个发生 & A与B的并集 \\ \hline A\cap B或AB & 事件A与事件B同时发生 & A与B的交集 \\ \hline A-B & 事件A发生而事件B不发生 & A与B的差集 \\ \hline AB=\varnothing & 事件A与事件B互不相容 & A与B没有相同的元素 \\ \hline \end{array}$

事件的运算定律
幂等律： $A\cup A=A$ ， $A\cap A=A$
交换律： $A\cup B=B\cup A$ ， $A\cap B=B\cap A$
结合律： $(A\cup B)\cup C=A\cup(B\cup C)$ ， $(A\cap B)\cap C=A\cap(B\cap C)$
分配律： $A\cap(B\cup C)=(A\cap B)\cup(A\cap C)$ ， $A\cup(B\cap C)=(A\cup B)\cap(A\cup B)$
德摩根率： $\overline{A\cup B}=\overline A\cap\overline B$ ， $\overline{A\cap B}=\overline A\cup\overline B$

1.2 概率和频率

概率定义：随机事件A在n次试验中发生的频率为 $f_n(A)=\frac{n_A}{n}$ ，其中 $n_A$ 是A发生的次数（频数），n是总试验次数。随着试验次数的增多， $f_n(A)$ 趋于稳定值p，称随机事件A的概率为P(A)=p。

概率特性：
非负性：对任意的随机事件A，P(A) $\ge$ 0
规范性： $P(\Omega)=1$
可加性：对于N个互斥的事件A， $i=1,\cdots,N$ ，其和事件的概率应该等于它们的概率之和。

例一

下面写一个程序模拟硬币抛掷，从 0 和 1 中随机取一个，0 代表正面，统计出现 0 的次数，再和试验次数比起来计算正面出现的频率。

import random

def coin_trial(times):
    heads = 0
    for i in range(times):
        if random.randint(0, 1) == 0:
            print
            heads += 1
    return heads

def simulate(times):
    return coin_trial(times) / times

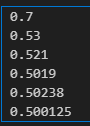
print(simulate(10))
print(simulate(100))
print(simulate(1000))
print(simulate(10000))
print(simulate(100000))
print(simulate(1000000))

在试验次数为 10 时结果经常偏差很大，时高时低，当次数增大到一定层度后，结果就稳定趋向 0.5 了。

1.3 古典概型

古典概型中样本空间只有有限个样本点，并且每个样本点构成的基本事件发生的概率是相同的，因此古典概型又称为等可能概型。
定义：样本空间 $\Omega=\{\omega_1,\omega_2,\cdots,\omega_n\}$ ， $P(\{\omega_i\})=\frac{1}{n}$ ， $i=1,2,3,\cdots,n$ 。

2 条件概率

设A、B为随机事件，且P(A)>0，则有
$P(B|A)=\frac{P(AB)}{P(A)}$
称P(B|A)为在事件A发生的条件下，事件B发生的概率。

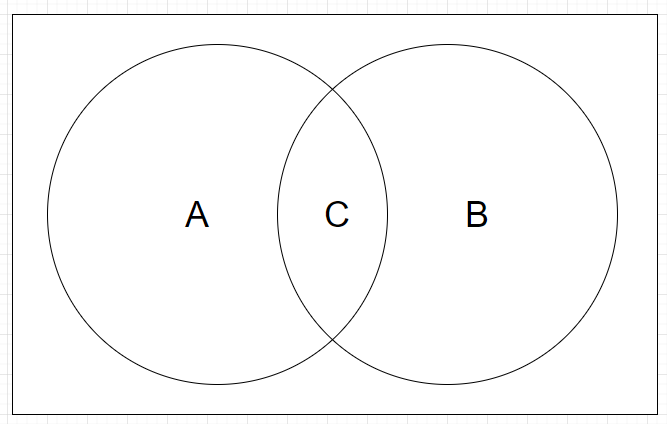
结合图片来理解，A是左边的圆，B是右边的圆，C是A和B的公共部分，即 $C=AB=A\cap B$ 。
(B|A)就是在A发生的情况下，C发生的概率，即 $P(B|A)=\frac{\frac{n(AB)}{n(\Omega)}}{\frac{n(A)}{n(\Omega)}}=\frac{n(C)}{n(A)}$

例一

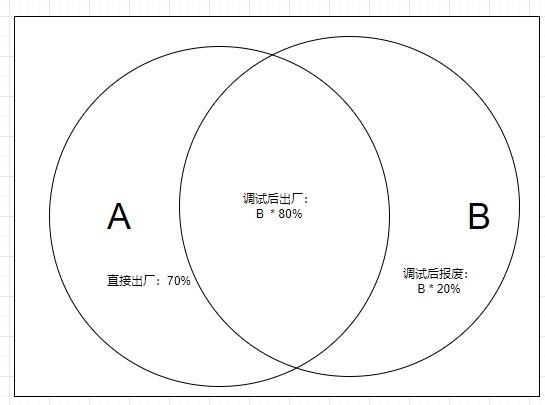
某厂生产的产品能直接出厂的概率为 70%，余下的 30% 的产品要调试后再定。已知调试后有 80% 的产品可以出厂，20% 的产品要报废，求该厂产品的报废率。

设 A 为最终都可以出厂的，设 B 为要调试的。A 分为可以直接出厂的和需要调试后才能出厂的两部分，B 分为调试后可以出厂的和调试后报废的两部分，报废的只来源于调试后报废的，调试后报废的占调试的 20%，调试的占总的 30%，那么P(调试后报废)=30% x 20%=6%。

例二

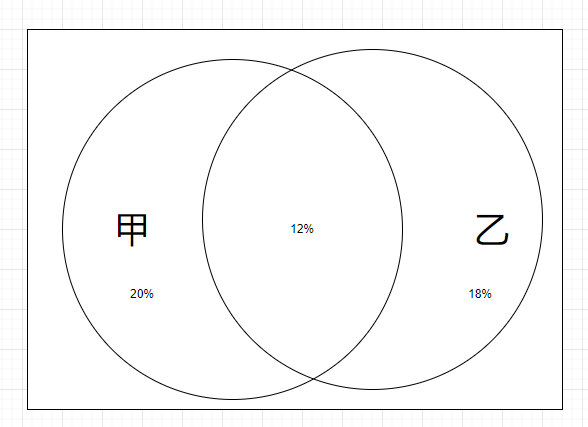
甲乙两地雨天的概率分别为20%和18%，两地同时下雨的概率为12%，计算：
（1）乙为雨天，甲为雨天的概率。
（2）甲为雨天，乙为雨天的概率。

设 A={甲为雨天}，B={乙为雨天}
则P(A)=0.2，P(B)=0.18，P(AB)=0.12

答（1）
$P(A|B)=\frac{P(AB)}{P(B)}=\frac{0.12}{0.18}=\frac{2}{3}$

答（2）
$P(B|A)=\frac{P(AB)}{P(A)}=\frac{0.12}{0.2}=\frac{3}{5}$

2.1 事件独立性

随机事件之间互相独立，不会影响。比如投掷一枚硬币，设第一次为正面为事件 A，第二次为正面为事件 B。问投掷两次，第一次为正面的情况下，第二次也为正面的概率，会发现第一次的结果完全不会影响第二次的结果，不管第一次结果是正面还是反面，第二次的为正面的概率还是 0.5。则有
$P(B|A)=\frac{P(AB)}{P(A)}=P(B)$
$P(AB)=P(A)P(B)$

定义：设A、B两事件满足等式 $P(AB)=P(A)P(B)$ ，则称事件 A 与事件 B 相互独立。

例一

甲、乙两人射击同一目标，甲射中的概率为 0.8，乙射中的概率为 0.7，求目标被射中的概率。

设 A={甲射中}，B={乙射中}，C={目标被射中}
P(A)=0.8，p(B)=0.7， $C=A\cup B$ ，P(C)=P(A)+P(B)-P(AB)
A、B 相互独立有 P(AB)=P(A)P(B)=0.56
P(C)=0.8+0.7-0.56=0.94

2.2 独立试验

重复独立试验是指在相同的条件下将试验 E 重复进行，且每次试验是独立进行的，即每次试验结果出现的概率不受其它各次试验结果的影响。
如果一个随机试验 E 只产生两个结果 A 和 $\overline{A}$ ，则称 E 为伯努利试验，将 E 重复进行 n 次，称为 n 重伯努利试验，也称为伯努利概型。

定义：n 重伯努利试验中，如果每次试验中事件 A 发生的概率为 P(A)=p，0<p<1，则在 n 重伯努利试验中事件 A 恰好发生 k 次的概率为 $P_n(k)=C_n^kp^k(1-q)^{n-k}$ ，k=1,2, $\cdots$ ,n。

例一

抛硬币试验中，求抛出 49 个正面，31 个反面的概率。

相当于进行 80 重伯努利试验，X 记为抛出正面的次数，有
$P\{X=49\}=C_{80}^{49}0.5^{49}0.5^{31}\approx0.011836$

注：排列组合计算参考：https://blog.iyatt.com/?p=10812

数学与计算机（3）- 概率论（停写）

作者IYATT-yx