阅读量： 80

最近更新于 2024-05-06 07:58

1 心形线

 $\begin{array}{l} \rho=a(1-\cos\theta)（a>0，\theta\in[0,2\pi]） \\ \\ x^2+y^2+ax=a\sqrt{x^2+y^2}（a\gt0）\\ \\ \begin{cases} x=a(1-\cos\theta)\cos\theta \\ y=a(1-\cos\theta)\sin\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)

rho = alpha * (1 - np.cos(theta))

plt.polar(theta, rho, color='r')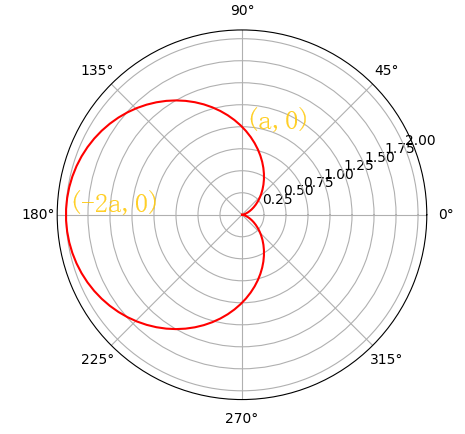

 $\begin{array}{l} \rho=a(1+\cos\theta)（a>0，\theta\in[0,2\pi]） \\ \\ x^2+y^2-ax=a\sqrt{x^2+y^2}（a\gt0）\\ \\ \begin{cases} x=a(1+\cos\theta)\cos\theta \\ y=a(1+\cos\theta)\sin\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)

rho = alpha * (1 + np.cos(theta))

plt.polar(theta, rho, color='r')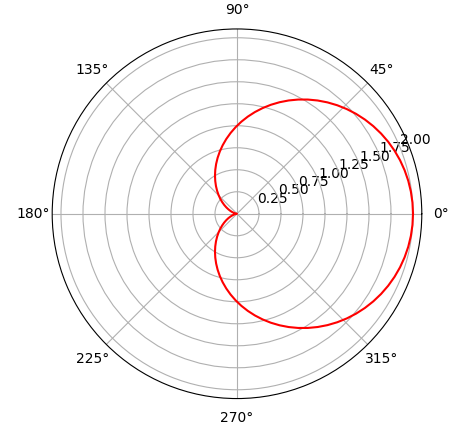

 $\begin{array}{l} \rho=a(1-\sin\theta)（a>0，\theta\in[0,2\pi]） \\ \\ x^2+y^2+ay=a\sqrt{x^2+y^2}（a\gt0）\\ \\ \begin{cases} x=a(1-\sin\theta)\cos\theta \\ y=a(1-\sin\theta)\sin\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)

rho = alpha * (1 - np.sin(theta))

plt.polar(theta, rho, color='r')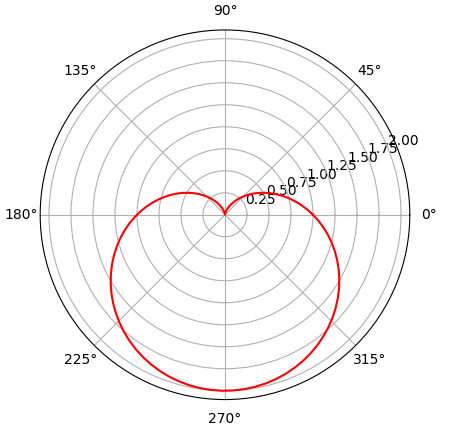

 $\begin{array}{l} \rho=a(1+\sin\theta)（a>0，\theta\in[0,2\pi]） \\ \\ x^2+y^2-ay=a\sqrt{x^2+y^2}（a\gt0）\\ \\ \begin{cases} x=a(1+\sin\theta)\cos\theta \\ y=a(1+\sin\theta)\sin\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)

rho = alpha * (1 + np.sin(theta))

plt.polar(theta, rho, color='r')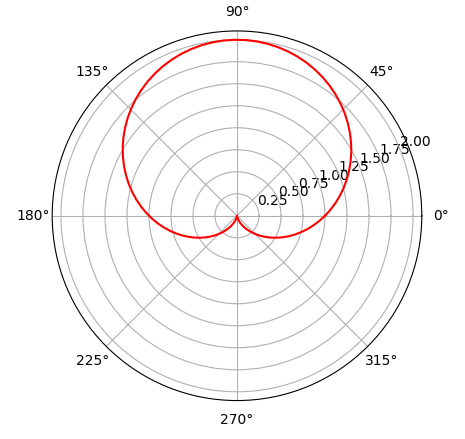

2 阿基米德螺线

 $\begin{array}{l} r=a\theta（r\gt0，\theta\ge0）(a\gt0，\theta\in[0,+\infty)) \\ \\ \begin{cases} x=a\theta\cos\theta \\ y=a\theta\sin\theta \end{cases} (a\gt0，\theta\in[0,+\infty)) \end{array}$

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)
rho = alpha * theta

x = rho * np.cos(theta)
y = rho * np.sin(theta)

plt.axis('equal')
plt.plot(x, y, color='r')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')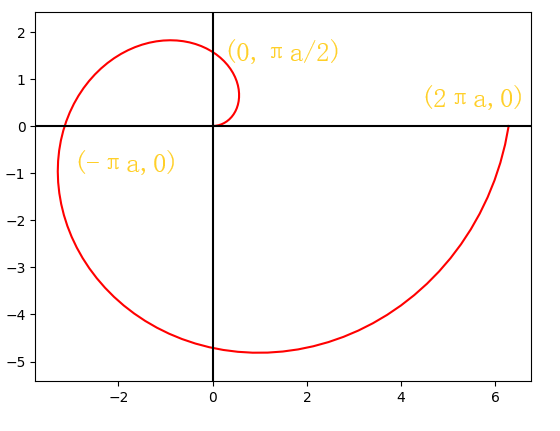

3 星形线

3.1 方程

 $\begin{array}{l} \rho=\frac{1}{(\cos^\frac{2}{3}\theta+\sin^\frac{2}{3})^\frac{3}{2}}（a>0，\theta\in[0,2\pi]）\\ \\ x^\frac{2}{3}+y^\frac{2}{3}=a^\frac{2}{3}（a\gt0）\\ \\ \begin{cases} x = a\cos^3\theta \\ y = a\sin^3\theta \end{cases} （a>0，\theta\in[0,2\pi]） \end{array}$

3.2 图像

import matplotlib.pyplot as plt
import numpy as np

alpha = 1
theta = np.linspace(0, 2 * np.pi, 100)
x = alpha * np.cos(theta)**3
y = alpha * np.sin(theta)**3

plt.axis('equal')
plt.plot(x, y, color='r')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')

3.3 弧长

弧微分参考：https://blog.iyatt.com/?p=10934#%E6%9B%B2%E7%BA%BF%E5%92%8C%E5%BC%A7%E5%BE%AE%E5%88%86%E5%92%8C%E6%9B%B2%E7%8E%87

 $\begin{array}{l} y=(a^\frac{2}{3} - x^\frac{2}{3})^\frac{3}{2} \\ \\ y'=\frac{3}{2}(a^\frac{2}{3} - x^\frac{2}{3})^\frac{1}{2}(-\frac{2}{3}x^{-\frac{1}{3}})=-(a^\frac{2}{3} - x^\frac{2}{3})^\frac{1}{2}x^{-\frac{1}{3}} \\ \\ \begin{aligned} L&=4\int_0^a\sqrt{1+y'^2}dx \\ &=4\int_0^a\sqrt{1+(a^\frac{2}{3} - x^\frac{2}{3})x^{-\frac{2}{3}}}dx \\ &=4\int_0^a|a^\frac{1}{3}x^{-\frac{1}{3}}|dx \\ &=4\times a^\frac{1}{3}\times\frac{3}{2}x^\frac{2}{3}|_0^a \\ &=6a \end{aligned} \end{array}$

3.4 平面封闭图形面积

 $\begin{aligned} A&=4\int_0^aydx \\ &=4\int_0^a(a^\frac{2}{3}-x^\frac{2}{3})^\frac{3}{2} \\ &\xlongequal{x=a\sin^3\theta}12a\int_0^\frac{\pi}{2}(a^\frac{2}{3}-a^\frac{2}{3}\sin^2\theta)^\frac{3}{2}\sin^2\theta\cos\theta d\theta \\ &=12a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta d\theta \\ &=12a^2\int_0^\frac{\pi}{2}\cos^4\theta(1-\cos^2\theta)d\theta \\ &=12a^2(\int_0^\frac{\pi}{2}\cos^4\theta d\theta-\int_0^\frac{\pi}{2}\cos^6\theta d\theta) \\ &\xlongequal{Wallis公式}12a^2(\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}-\frac{5}{6}\times\frac{3}{4}\times\frac{1}{2}\times\frac{\pi}{2}) \\ &=\frac{3}{8}\pi a^2 \end{aligned}$

3.5 旋转体

将图形绕 x 轴旋转一周

%matplotlib widget
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
from matplotlib.animation import FuncAnimation

alpha = 2

# 星形线参数方程
def star(t):
    x = alpha * np.cos(t)**3
    y = alpha * np.sin(t)**3
    return x, y

# 创建一个三维坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

t = np.linspace(0, 2 * np.pi, 100)
x, y = star(t)

cmap = plt.get_cmap('rainbow')

# 定义初始化函数，清空当前帧
def init():
    ax.clear()
    return ax,

# 定义更新函数，绘制每一帧的图形
def update(frame):
    # 清空当前帧
    ax.clear()
    # 设置坐标轴的标签和范围
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    ax.set_xlim(-1.5, 1.5)
    ax.set_ylim(-1.5, 1.5)
    ax.set_zlim(-1.5, 1.5)
    # 绘制三个坐标轴
    ax.plot([0, 5], [0, 0], [0, 0], color='r', label='X')
    ax.plot([0, 0], [0, 5], [0, 0], color='g', label='Y')
    ax.plot([0, 0], [0, 0], [0, 5], color='b', label='Z')
    # 计算旋转后的y和z坐标
    y_rot = y * np.cos(frame)
    z_rot = y * np.sin(frame)
    # 绘制旋转后的曲线
    ax.plot(x, y_rot, zs=z_rot, zdir='z', color=cmap(frame / (2*np.pi)))

# 创建动画对象，设置帧数，间隔和重复播放
ani = FuncAnimation(fig, update, frames=np.linspace(0, 2 * np.pi, 100), init_func=init, interval=10, repeat=True)

%matplotlib widget
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

alpha = 2

# 星形线参数方程
def star(t):
    x = alpha * np.cos(t)**3
    y = alpha * np.sin(t)**3
    return x, y

# 创建一个三维坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

t = np.linspace(0, 2 * np.pi, 100)
x, y = star(t)

cmap = plt.get_cmap('rainbow')

# 将星形线以 x 轴为中心线旋转一周，得到三维图形
for angle in np.linspace(0, 2 * np.pi, 100):
    # 计算旋转后的 y 和 z 坐标
    y_rot = y * np.cos(angle)
    z_rot = y * np.sin(angle)
    ax.plot(x, y_rot, zs=z_rot, zdir='z', color=cmap(angle / (2*np.pi)))

# 设置坐标轴的标签和范围
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_xlim(-1.5, 1.5)
ax.set_ylim(-1.5, 1.5)
ax.set_zlim(-1.5, 1.5)

ax.plot([0, 5], [0, 0], [0, 0], color='r', label='X')
ax.plot([0, 0], [0, 5], [0, 0], color='g', label='Y')
ax.plot([0, 0], [0, 0], [0, 5], color='b', label='Z')

3.5.1 体积

 $\begin{array}{l} y^2=(a^\frac{2}{3} - x^\frac{2}{3})^3 \\ \begin{aligned} V&=2\pi\int_0^ay^2dx \\ &=2\pi\int_0^a(a^\frac{2}{3} - x^\frac{2}{3})^3dx \\ &\xlongequal{x=a\sin^3\theta}2\pi\int_0^a(a^\frac{2}{3}-a^\frac{2}{3}\sin^2\theta)^3\cdot3a\sin^2\theta\cos\theta d\theta \\ &=6\pi a^3\int_0^a\cos^7\theta\sin^2\theta d\theta \\ &=6\pi a^3\int_0^a\cos^7\theta(1-\cos^2\theta)d\theta \\ &=6\pi a^3\int_0^a(\cos^7\theta-\cos^9\theta)d\theta \\ &\xlongequal{Wallis公式}6\pi a^3(\frac{6\times4\times2}{7\times5\times3}-\frac{8\times6\times4\times2}{9\times7\times5\times3}) \\ &=\frac{32}{105}\pi a^3 \end{aligned} \end{array}$

3.5.2 表面积

 $\begin{aligned} S&=2\times2\pi\int_0^a|y|\sqrt{1+y'^2}dx \\ &=4\pi\int_0^a|(a^\frac{2}{3} - x^\frac{2}{3})^\frac{3}{2}|\sqrt{1+(a^\frac{2}{3} - x^\frac{2}{3})x^{-\frac{2}{3}}}dx \\ &\xlongequal{x=a\sin^3\theta}4\pi\int_0^\frac{\pi}{2}|a\cos^3\theta|\sqrt{1+\cos^2\theta\sin^{-2}\theta}\times3a\sin^2\theta\cos\theta d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta\sqrt{1+\cot^2\theta}d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta\sin^2\theta|\csc\theta|d\theta \\ &=12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta|\sin\theta|d\theta \\ &=-12\pi a^2\int_0^\frac{\pi}{2}\cos^4\theta d\cos\theta \\ &=-12\pi a^2\cdot\frac{1}{5}\cos^5\theta|_0^\frac{\pi}{2} \\ &=\frac{12}{5}\pi a^2 \end{aligned}$

4 伯努利双扭线

 $\begin{array}{l} r^2=a^2\cos2\theta（\theta\in[-\frac{\pi}{4},\frac{\pi}{4}]\cup[\frac{3\pi}{4},\frac{5\pi}{4}]，a\gt0）\\ \\ (x^2+y^2)^2=2a^2(x^2-y^2)（a\gt0） \end{array}$

import numpy as np
import matplotlib.pyplot as plt

alpha = 1
theta = np.concatenate((
    np.linspace(-np.pi / 4, np.pi / 4, 100),
    np.linspace(3 * np.pi / 4, 5 * np.pi / 4, 100)
))

rho = alpha * np.sqrt(np.abs(np.cos(2 * theta)))

plt.polar(theta, rho, color='r')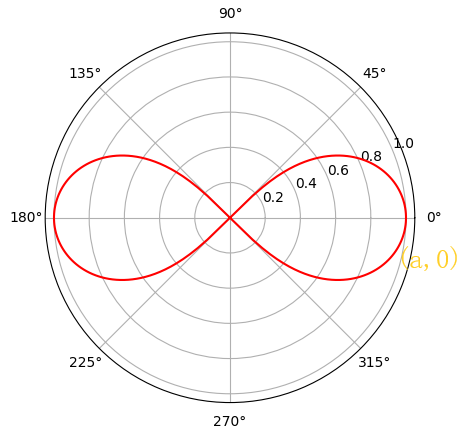

 $\begin{array}{l} r^2=a^2\sin2\theta（\theta\in[0,\frac{\pi}{2}]\cup[\pi,\frac{3\pi}{2}]，a\gt0） \\ \\ (x^2+y^2)^2=2a^2xy（a\gt0） \end{array}$

import numpy as np
import matplotlib.pyplot as plt

alpha = 1
theta = np.concatenate((
    np.linspace(0, np.pi / 2, 100),
    np.linspace(np.pi, 3 * np.pi / 2, 100)
))

rho = alpha * np.sqrt(np.abs(np.sin(2 * theta)))

plt.polar(theta, rho, color='r')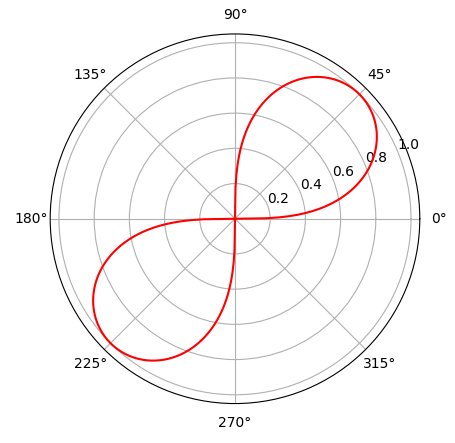

5 摆线

 $\begin{cases} x=a(\theta-\sin\theta) \\ y=a(1-\cos\theta) \end{cases} （a\gt0）$

import numpy as np
import matplotlib.pyplot as plt

alpha = 1
theta = np.linspace(0, 4 * np.pi, 100)

x = alpha * (theta - np.sin(theta))
y = alpha * (1 - np.cos(theta))

plt.axis('equal')
plt.plot(x, y, color='r')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.axhline(y=2 * alpha, color='b')
plt.axvline(x=np.pi * alpha, color='b')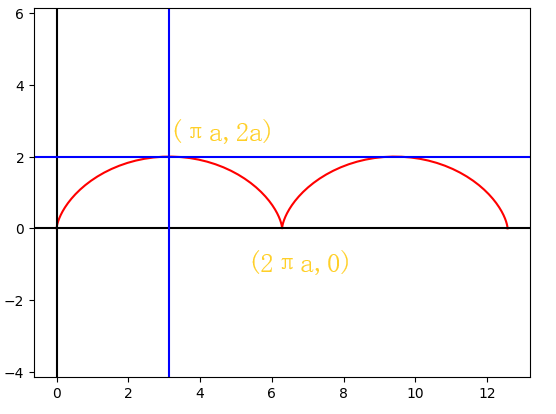

高等数学常用曲线（编辑中）