最近更新于 2024-05-05 12:32

定义式

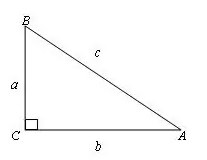
\begin{array}{l l l l}
正弦 & \sin A=\frac{a}{c} & 余割 & \csc A=\frac{c}{a} \\
余弦 & \cos A=\frac{b}{c} & 正割 & \sec A=\frac{c}{b} \\
正切 & \tan A=\frac{a}{b} & 余切 & \cot A=\frac{b}{a}
\end{array}

函数关系

倒数

\begin{array}{l}
\tan\alpha \cot\alpha=1 \\
\sin\alpha \csc\alpha=1 \\
\cos\alpha \sec\alpha=1
\end{array}

商数

\begin{array}{l}
\tan\alpha=\frac{\sin\alpha}{\cos\alpha} \\
\cot\alpha=\frac{\cos\alpha}{\sin\alpha}
\end{array}

平方

\begin{array}{l}
\sin^2\alpha+\cos^2\alpha=1 \\
1+\tan^2\alpha=\sec^2\alpha \\
1+\cot^2\alpha=\csc^2\alpha
\end{array}

和

\begin{array}{l}
\arcsin x+\arccos x=\frac{\pi}{2} \\
\arctan x+arccot\ =\frac{\pi}{2}
\end{array}

诱导公式

公式一

k\in Z

\begin{array}{l}
\sin(2k\pi+\alpha)=\sin\alpha \\
\cos(2k\pi+\alpha)=\cos\alpha \\
\tan(2k\pi+\alpha)=\tan\alpha \\
\cot(2k\pi+\alpha)=\cot\alpha
\end{array}

公式二

\begin{array}{l}
\sin(\pi+\alpha)=-\sin\alpha \\
\cos(\pi+\alpha)=-\cos\alpha \\
\tan(\pi+\alpha)=\tan\alpha \\
\cot(\pi+\alpha)=\cot\alpha
\end{array}

公式三

\begin{array}{l}
\sin(-\alpha)=-\sin\alpha \\
\cos(-\alpha)=\cos\alpha \\
\tan(-\alpha)=-\tan\alpha \\
\cot(-\alpha)=-\cot\alpha
\end{array}

公式四

\begin{array}{l}
\sin(\pi-\alpha)=\sin\alpha \\
\cos(\pi-\alpha)=-\cos\alpha \\
\tan(\pi-\alpha)=-\tan\alpha \\
\cot(\pi-\alpha)=-\cot\alpha
\end{array}

公式五

\begin{array}{l}
\sin(2\pi-\alpha)=-\sin\alpha \\
\cos(2\pi-\alpha)=\cos\alpha \\
\tan(2\pi-\alpha)=-\tan\alpha \\
\cot(2\pi-\alpha)=-\cot\alpha
\end{array}

公式六

\begin{array}{l}
\sin(\frac{\pi}{2}+\alpha)=\cos\alpha \\
\cos(\frac{\pi}{2}+\alpha)=-\sin\alpha \\
\tan(\frac{\pi}{2}+\alpha)=-\cot\alpha \\
\cot(\frac{\pi}{2}+\alpha)=-\tan\alpha \\
\ \\
\sin(\frac{\pi}{2}-\alpha)=\cos\alpha \\
\cos(\frac{\pi}{2}-\alpha)=\sin\alpha \\
\tan(\frac{\pi}{2}-\alpha)=\cot\alpha \\
\cot(\frac{\pi}{2}-\alpha)=\tan\alpha \\
\ \\
\sin(\frac{3\pi}{2}+\alpha)=-\cos\alpha \\
\cos(\frac{3\pi}{2}+\alpha)=\sin\alpha \\
\tan(\frac{3\pi}{2}+\alpha)=-\cot\alpha \\
\cot(\frac{3\pi}{2}+\alpha)=-\tan\alpha \\
\ \\

\sin(\frac{3\pi}{2}-\alpha)=-\cos\alpha \\
\cos(\frac{3\pi}{2}-\alpha)=-\sin\alpha \\
\tan(\frac{3\pi}{2}-\alpha)=\cot\alpha \\
\cot(\frac{3\pi}{2}-\alpha)=\tan\alpha
\end{array}

规律

奇变偶不变，符号看象限
\frac{\pi}{2}k+\alpha，k\in Z

各象限符号 \\
\ \\
sin \\
\begin{array}{c | c}
+ & + \\
\hline
- & -
\end{array}
\ \\
cos \\
\begin{array}{c | c}
- & + \\
\hline
- & +
\end{array}
\ \\
tan \\
\begin{array}{c | c}
- & + \\
\hline
+ & -
\end{array}
\ \\
cot \\
\begin{array}{c | c}
- & + \\
\hline
+ & -
\end{array}

解释
k 为奇数，则 sin 变 cos，cos 变 sin，tan 变 cot，cot 变 tan，k 为偶数不变
将\alpha 当作锐角，\frac{\pi}{2}k+\alpha在哪个象限，对应三角函数正负

和差公式

二角和差

\begin{array}{l}
\sin(\alpha+\beta)=\sin\alpha \cos\beta+\cos\alpha \sin\beta \\
\sin(\alpha-\beta)=\sin\alpha \cos\beta - \cos\alpha \sin\beta \\
\cos(\alpha+\beta)=\cos\alpha \cos\beta - \sin\alpha \sin\beta \\
\cos(\alpha-\beta)=\cos\alpha \cos\beta + \sin\alpha \sin\beta \\
\ \\
\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha \tan\beta} \\
tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha \tan\beta} \\
cot(\alpha+\beta)=\frac{1-\tan\alpha \tan\beta}{\tan\alpha+\tan\beta} \\
cot(\alpha-\beta)=\frac{1+\tan\alpha \tan\beta}{\tan\alpha-\tan\beta}
\end{array}

和差化积

\begin{array}{l}
\sin\alpha+\sin\beta=2\sin\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} \\
\sin\alpha-\sin\beta=2\cos\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2} \\
\cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2} \\
\cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}{2}\sin\frac{\alpha-\beta}{2} \\
\tan\alpha+\tan\beta=\frac{\sin(\alpha+\beta)}{\cos\alpha\cos\beta}
\end{array}

积化和差

\begin{array}{l}
①\sin\alpha\cos\beta=\frac{1}{2}[\sin(\alpha+\beta)+\sin(\alpha-\beta)] \\
②\cos\alpha\sin\beta=\frac{1}{2}[\sin(\alpha+\beta)-\sin(\alpha-\beta)] \\
③\sin\alpha\sin\beta=-\frac{1}{2}[\cos(\alpha+\beta)-\cos(\alpha-\beta)] \\
④\cos\alpha\cos\beta=\frac{1}{2}[\cos(\alpha+\beta)+\cos(\alpha-\beta)] \\
\end{array}

倍角公式

二倍角公式

\begin{array}{l}
\sin2\alpha=2\sin\alpha\cos\alpha \\
\cos2\alpha=\cos^2\alpha-\sin^2\alpha=2\cos^2\alpha-1=1-2\sin^2\alpha \\
\tan2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha} \\
\end{array}

三倍角公式

\begin{array}{l}
\sin3\alpha=3\sin\alpha-4\sin^3\alpha=4\sin\alpha\sin(\frac{\pi}{3}-\alpha)\sin(\frac{\pi}{3}+\alpha) \\
\cos3\alpha=4\cos^3\alpha-3\cos\alpha=4\cos\alpha\cos(\frac{\pi}{3}-\alpha)\cos(\frac{\pi}{3}+\alpha) \\
\tan3\alpha=\tan\alpha\tan(\frac{\pi}{3}-\alpha)\cos(\frac{\pi}{3}+\alpha)
\end{array}

半角公式

\begin{array}{l}
\sin\frac{\alpha}{2}=\pm\sqrt{\frac{1-\cos\alpha}{2}} ，（\sin^2\alpha=\frac{1-\cos2\alpha}{2}）\\
\cos\frac{\alpha}{2}=\pm\sqrt{\frac{1+\cos\alpha}{2}}， （\cos^2\alpha=\frac{1+\cos2\alpha}{2}）\\
\tan\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{1-\cos\alpha}{\sin\alpha}=\pm\sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}} \\
\cot\frac{\alpha}{2}=\frac{1+\cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1-\cos\alpha}=\pm\sqrt{\frac{1+\cos\alpha}{1-\cos\alpha}}
\end{array}

符号由 \frac{\alpha}{2} 所在象限决定

辅助角公式

\begin{array}{l}
a\sin\alpha+b\cos\alpha=\sqrt{a^2+b^2}sin(\alpha+\phi)， \\
\phi=\arctan\frac{b}{a}
\end{array}

正弦定理

在任意△ABC中，角A、B、C所对的边长分别为a、b、c，三角形的外接圆半径为R，则有
\frac{a}{\sin A}=\frac{b}{\sin b}=\frac{c}{\sin C}=2R
可得

\begin{array}{l}
S=\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A=\frac{abc}{4R} \\
a=2R\sin A，b=2R\sin B，c=2R\sin C \\
a:b:c=\sin A:\sin B:\sin C
\end{array}

余弦定理

\begin{array}{l}
a^2=b^2+c^2-2bc\cos A \\
b^2=a^2+c^2-2ac\cos B \\
c^2=a^2+b^2-2ab\cos C \\
\ \\
\cos A=\frac{b^2+c^2-a^2}{2bc} \\
\cos B=\frac{a^2+c^2-b^2}{2ac} \\
\cos C=\frac{a^2+b^2-c^2}{2ab}
\end{array}