最近更新于 2024-05-05 14:18
热能传递的三种基本方式
\begin{cases}
热传导 \\
热对流 \\
热辐射
\end{cases}注:单位时间内通过某一给定面积的热量称为热流量,记为\Phi,单位为 W。通过单位面积的热流量称为热流密度,记为 q,单位为 W/m^2。
热传导
物体各部分之间不发生相对位移时,依靠分子、原子及自由电子等微观粒子的热运动而产生的热能传递。
通过对大量实际导热问题的经验提炼,导热现象的规律已总结为傅里叶定律(导热基本定律)。
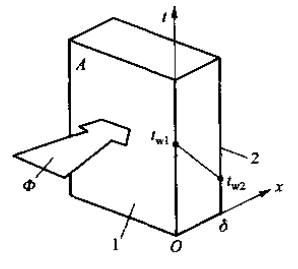
\Phi=-\lambda A\frac{dt}{dx}
\lambda称为热导率(或导热系数),单位为W/(m\cdot K)
A 平板面积
一维稳态中推导可得:
\Phi=\lambda A\frac{t_{w1}-t_{w2}}{\delta}
推导过程:
一维稳态常物性无内热源导热微分方程:\\
\frac{d^2t}{dx^2}=0 \\
连续两次积分有:\\
t=C_1x+C_2 \\
代入边界条件:
\begin{cases}
x=0时,t=t_{w1} \\
x=\delta时,t=t_{w2}
\end{cases}
,可知
\begin{cases}
C_1=\frac{t_{w2}-t_{w1}}{\delta} \\
C_2=t_{w2}
\end{cases}
\\
则 \frac{dt}{dx}=\frac{t_{w2}-t_{w1}}{\delta}, 代入到傅里叶定律中有 \\
\Phi=-\lambda A\frac{dt}{dx}=\lambda A\frac{t_{w1}-t_{w2}}{\delta}热对流
由于液体的宏观运动而引起的流体各部分之间发生相对位移,冷、热流体相互掺混所导致的热量传递过程。
热对流仅能发生在流体中,而且用于流体中分子同时进行着不规则热运动,因而热对流必然伴随有热传导现象。工程上特别感兴趣的是流体流过一个物体表面时流体与物体表面间的热量传递过程,并称之为对流传热,以区别于一般意义上的热对流。这里只讨论对流传热(也称对流换热)。
对流传热的基本计算式是牛顿冷却公式:
\Phi=hA\Delta t
\Delta t是壁面温度和流体温度之差
h 称为表面传热系数,单位是W/(m^2\cdot K)。
热辐射
物体通过电磁波来传递能量的方式称为辐射。物体会因为各种原因发出辐射能,其中因为热的原因而发出的辐射能的现象为热辐射。
黑体(能吸收投入其表面上的所有热辐射能量的物体)在单位时间内发出的热辐射能量由 Stefan-Boltzmann 定律(四次方定律)揭示:
\Phi=A\sigma T^4
T 黑体的热力学温度,单位 K
\sigma Stefan-Boltzmann 常量,即黑体辐射常数,值为 5.67\times 10^{-8} W/(m^2\cdot K^4)
一切实际物体的辐射能力都小于同温度下的黑体。实际物体辐射热流量的计算可以采用 Stefan-Boltzmann 定律的修正形式:
\Phi=\epsilon A \sigma T^4
\epsilon 称为物体的发射率(黑度),与物体的种类和表面状态有关。
一种简单的热辐射传热情形是,一个表面积为 A,表面温度为T_1、发射率为\epsilon的物体被包容在一个表面温度为T_2的空腔内,此时该物体与空腔表面间的辐射换热量按下式计算:
\Phi=\epsilon A\sigma(T_1^4-T_2^4)
传热方程式
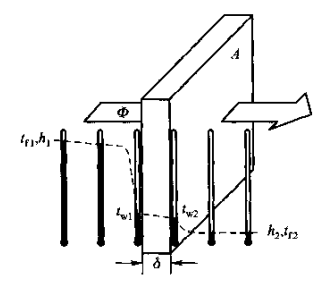
冷、热流体通过一块大平壁交换热量(仅分析稳态传热过程),首先从热流体到壁面高温侧的热量传递,然后从壁面高温侧到低温侧的热量传递,最后从壁面低温侧到冷流体的热量传递。三个环节的热流量表达式如下:
\begin{array}{l}
\Phi=Ah_1(t_{f1}-t_{w1}) \\
\Phi=\frac{A\lambda}{\delta}(t_{w1}-t_{w2}) \\
\Phi=Ah_2(t_{w2}-t_{f2})
\end{array}三式相加有:
\Phi=\frac{A(t_{f1}-t_{f2})}{\frac{1}{h_1}+\frac{\delta}{\lambda}+\frac{1}{h_2}}
也可表示成:
\Phi=Ak(t_{f1}-t_{f2})
k 称为传热系数,单位为 W/(m^2\cdot K),k=\frac{1}{\frac{1}{h_1}+\frac{\delta}{\lambda}+\frac{1}{h_2}}
\frac{1}{k}=\frac{1}{h_1}+\frac{\delta}{\lambda}+\frac{1}{h_2}
\frac{1}{Ak}=\frac{1}{Ah_1}+\frac{\delta}{A\lambda}+\frac{1}{Ah_2}
则可将 \Phi=Ak(t_{f1}-t_{f2}) 写为 \Phi=\frac{\Delta t}{1/Ak}
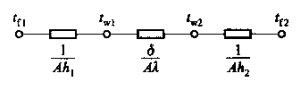
这个形式就和电学中的欧姆定律类似,1/(Ak) 具有类似电阻的作用,将其称为传热过程热阻。
参考
《传热学》 陶文铨 第五版
