最近更新于 2024-05-05 12:30

参考：

• https://blog.csdn.net/m0_46145808/article/details/106019301

1 逆分布函数法（Inverse Transform Method）

已知概率密度函数(Probability Density Function，PDF)： f(x)
得到 f(x) 的累积分布函数（Cumulative Density Function，CDF），也称分布函数：F(x)=\int_{-\infty}^xf(t)dt
得到 F(x) 的反函数（逆函数）(Inverse Cumulative Density Function，ICDF)：x=F^{-1}(y)
生成服从 U(0,1) 均匀分布的随机数 x（即概率取值在 0-1 范围），代入 ICDF 计算得到的值即为要求的随机数。

有些情况下人工求解 ICDF 比较困难，可以用 SymPy 库得到。
积分参考：https://blog.iyatt.com/?p=12906#7_%E7%A7%AF%E5%88%86
反函数参考：https://blog.iyatt.com/?p=14396
比如：

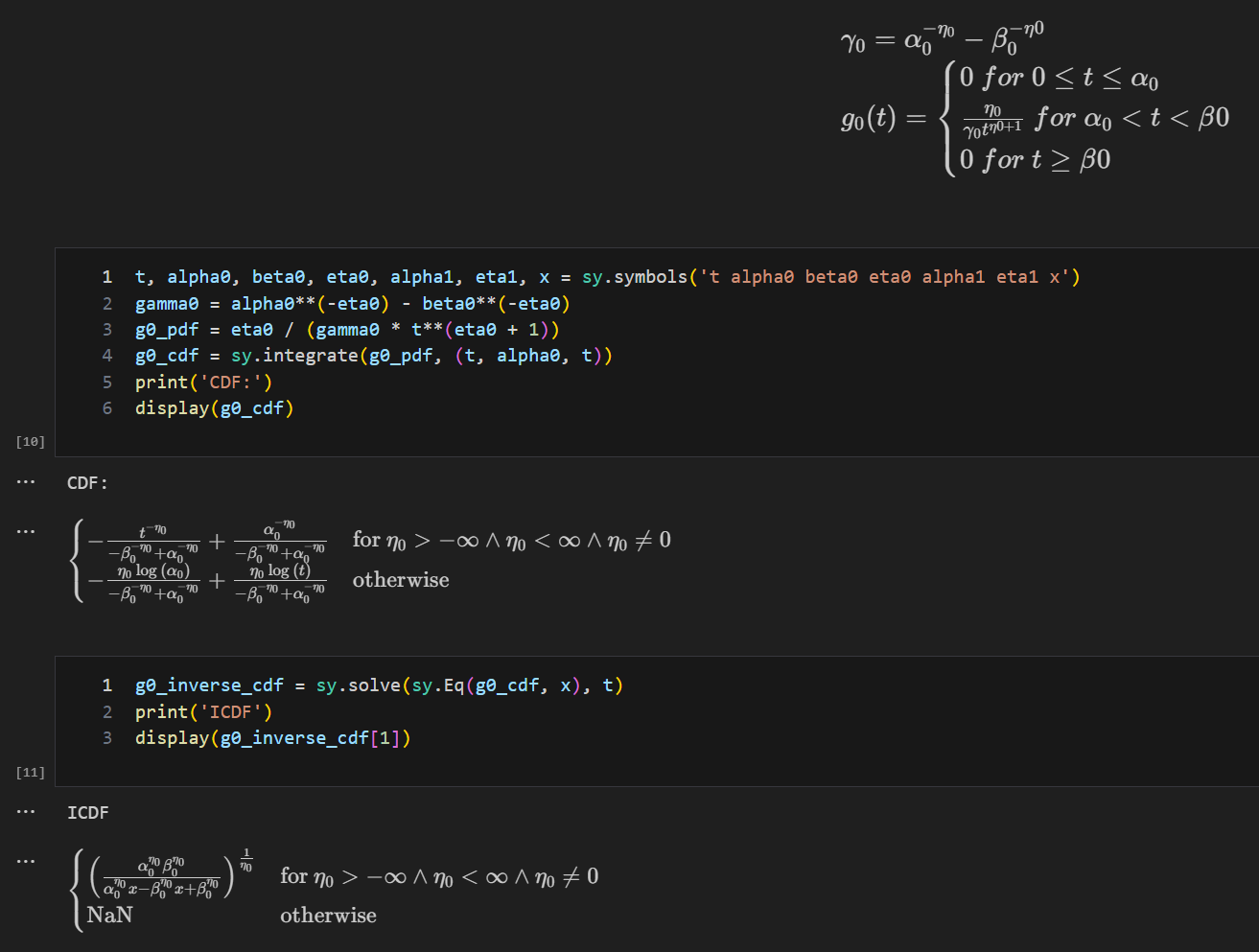
例一

PDF：f(x)=\sqrt{x},x\ge0
CDF：F(x)=\int_0^xf(t)dt=\frac{2}{3}t^{\frac{3}{2}}|_0^x=\frac{2}{3}x^{\frac{3}{2}}
ICDF：F^{-1}(x)=(\frac{3}{2}x)^{\frac{2}{3}}
对 ICDF，x 为服从 U(0,1) 均匀分布的随机数

import numpy as np
import matplotlib.pyplot as plt

def icdf(x):
    return (3 * x / 2)**(2 / 3)

random_list = list()
number = 10000
for i in range(number):
    p = np.random.uniform(0, 1)
    random_list.append(icdf(p))

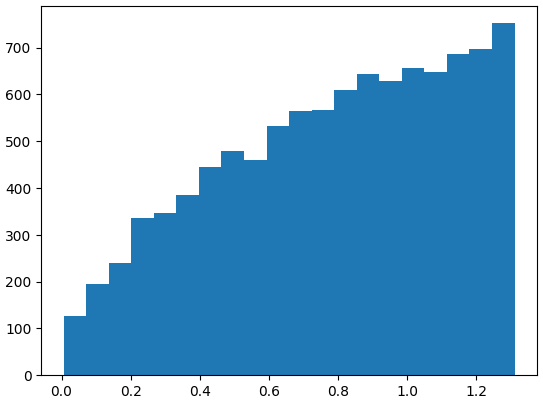
plt.hist(random_list, bins=20)

上面代码进行了 10000 次随机数生成，首先生成均匀分布的随机数，范围取值在 0-1（概率的范围），将生成的数代入 ICDF 计算出的值就是符合 PDF 的随机数。下面绘制了生成的 10000 个随机数的直方图，横坐标是数据的区间，纵坐标是对应的频数。

PDF 的函数曲线图像

import matplotlib.pyplot as plt
import numpy as np

def pdf(x):
    return  x**(1 / 2)

X = np.linspace(0, (3 / 2)**(2 / 3), 1000)
Y = pdf(X)
plt.plot(X, Y)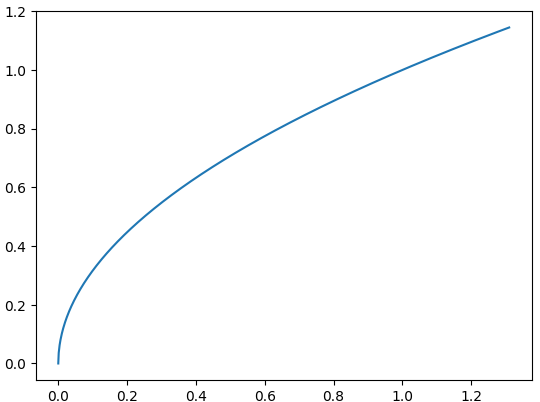

2 舍选法（Acceptance-Rejection Method）

这种方法理论上只要知道 PDF 就能用，而有些情况下，逆分布函数可能不存在或者难求，第一种方法就不那么适用。
已知 PDF 为 f(x)，如果要生成的随机数范围是 (a, b)，那么生成服从 U(a,b) 均匀分布的随机数 x，再生成服从 U(0,M) 的随机数 y（M 为f(x) 在(a,b)区间的最大取值，实际 M 这个位置的取值可以大于等于 M, 只是会降低效率，增大重复执行的可能）。当满足 y\le f(x)时，x 的值就是要生成的随机数，否则重复执行直到满足条件。

例一

PDF：f(x)=\sqrt{x},x\ge0
CDF：F(x)=\int_0^xf(t)dt=\frac{2}{3}t^{\frac{3}{2}}|_0^x=\frac{2}{3}x^{\frac{3}{2}}

令 CDF = 1，即概率的最大值，可得到 x 最大取值(\frac{3}{2})^{\frac{2}{3}}，代入 PDF 得到 PDF 最大取值 (\frac{3}{2})^{\frac{1}{3}}.
则生成随机数 x=U(0,(\frac{3}{2})^{\frac{2}{3}})，y=U(0,(\frac{3}{2})^{\frac{1}{3}})，再判断 y<f(x)，满足则取 x 的值作为随机数，不满足就重复执行。

import numpy as np
import matplotlib.pyplot as plt

def pdf(x):
    return x**(1 / 2)

random_list = list()
number = 10000
for i in range(number):
    while True:
        x = np.random.uniform(0, (3 / 2)**(2 / 3))
        y = np.random.uniform(0, (3 / 2)**(1 / 3))
        if y <= pdf(x):
            random_list.append(x)
            break

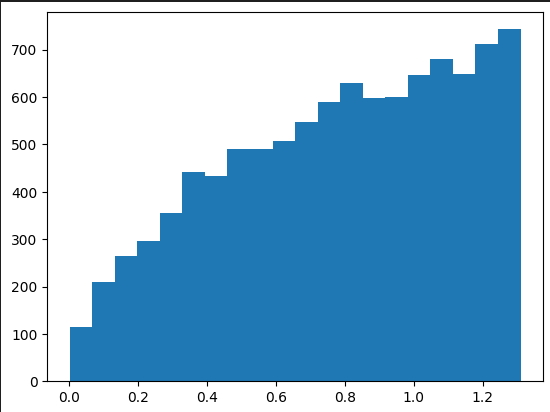
plt.hist(random_list, bins=20)

下图是生成的 10000 个随机数的分布图