最近更新于 2024-05-05 12:32

关系

可导（可微）一定连续，连续不一定可导（可微），不连续一定不可导（不可微）

可导

y=f(x) 在 x_0 的邻域内有定义且 \lim_{\Delta x\to0}\frac{\Delta x}{\Delta y}=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} 存在，则 f(x) 在 x_0 处可导。
f'(x_0)=y'|_{x=x_0}=\frac{dy}{dx}|_{x=x_0}=\lim_{\Delta x\to0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}

可微

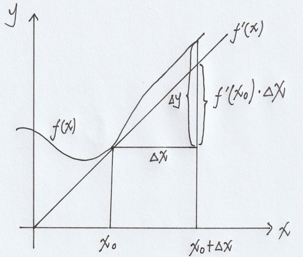
y=f(x) 在 x_0 的邻域内有定义，增量 \Delta y=f(x_0+\Delta x)-f(x_0) 可以表示为 \Delta y=A\Delta x+o(\Delta x)，其中 \Delta x\to0

A\Delta x 就是 y=f(x) 在 x_0 处的微分，即 dy=df(x)=A\Delta x
可微的充分必要条件就是可导，有 dy=f'(x_0)\Delta x=f'(x_0)dx

连续

y=f(x) 在 x_0 的邻域内有定义，\lim_{x\to x_0}f(x)=f(x_0) 时连续，即左右极限存在且等于函数值就连续

第一类间断点

只有两种

可去间断点

左右极限相等，但不等于函数值

跳跃间断点

左右极限不相等

第二类间断点

左右极限至少有一个不存在，这里只列举常见的两种

无穷间断点

左右极限有一个趋于无穷

振荡间断点

有界，但是没有极限

比如 \sin\frac{1}{x} 在 x\to0 时，值保持在 [-1,1] 范围，但是没有极限，是振荡的