最近更新于 2024-05-05 14:19
测试环境
gcc 9.4.0 – 64位
-no-pie -std=c17 -Wall -Werror=return-type -Werror=address -Werror=sequence-point -Werror=format-security -Wextra -pedantic -Wimplicit-fallthrough -Wsequence-point -Wswitch-unreachable -Wswitch-enum -Wstringop-truncation -Wbool-compare -Wtautological-compare -Wfloat-equal -Wshadow=global -Wpointer-arith -Wpointer-compare -Wcast-align -Wcast-qual -Wwrite-strings -Wdangling-else -Wlogical-op -Wconversion -g -O0 -lm
方法一:牛顿迭代法
#include <stdio.h>
#include <math.h>
double my_abs(double num)
{
if (num < 0)
{
return -num;
}
return num;
}
double my_sqrt(double num)
{
double epsilon = 0.000001; // 精度要求
double guess = 1.0; // 初始估计值
while (my_abs(guess * guess - num) > epsilon)
{
guess = ((num / guess) + guess) / 2;
}
return guess;
}
int main()
{
printf("my_sqrt\t\tsqrt\n");
printf("%lf\t%lf\n", my_sqrt(2), sqrt(2));
printf("%lf\t%lf\n", my_sqrt(3), sqrt(3));
printf("%lf\t%lf\n", my_sqrt(4), sqrt(4));
printf("%lf\t%lf\n", my_sqrt(5), sqrt(5));
printf("%lf\t%lf\n", my_sqrt(6), sqrt(6));
printf("%lf\t%lf\n", my_sqrt(7), sqrt(7));
printf("%lf\t%lf\n", my_sqrt(8), sqrt(8));
printf("%lf\t%lf\n", my_sqrt(9), sqrt(9));
printf("%lf\t%lf\n", my_sqrt(10), sqrt(10));
}
方法二:二分法
#include <stdio.h>
#include <math.h>
double my_abs(double num)
{
if (num < 0)
{
return -num;
}
return num;
}
double my_sqrt(double num)
{
double epsilon = 0.000001; // 精度
double low = 0;
double high = num;
double mid = (low + high) / 2;
while (my_abs(mid * mid - num) > epsilon)
{
if (mid * mid > num)
{
high = mid;
}
else
{
low = mid;
}
mid = (high + low) / 2;
}
return mid;
}
int main()
{
printf("my_sqrt\t\tsqrt\n");
printf("%lf\t%lf\n", my_sqrt(2), sqrt(2));
printf("%lf\t%lf\n", my_sqrt(3), sqrt(3));
printf("%lf\t%lf\n", my_sqrt(4), sqrt(4));
printf("%lf\t%lf\n", my_sqrt(5), sqrt(5));
printf("%lf\t%lf\n", my_sqrt(6), sqrt(6));
printf("%lf\t%lf\n", my_sqrt(7), sqrt(7));
printf("%lf\t%lf\n", my_sqrt(8), sqrt(8));
printf("%lf\t%lf\n", my_sqrt(9), sqrt(9));
printf("%lf\t%lf\n", my_sqrt(10), sqrt(10));
}
简单效率比较
测试条件,依次计算 2~10000000 之间整数的算数平方根,每计算一个 printf 输出一次。
牛顿迭代法:
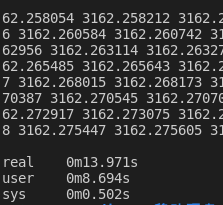
二分法:
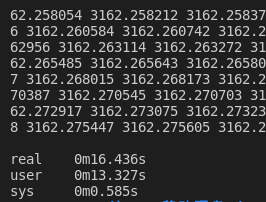
相比而言,牛顿迭代法的效率似乎更高一些。如果在两种算法的循环中加入计数就会发现,二分法通常循环次数更多,总体而言消耗时间也就更多。在计算单个数据的算数平方根的时候可能看不出来,但是像上面达到千万级的数据计算时,累加起来就会看出明显的差距了。
算数平方根计算
