斐波那契数列

最近更新于 2024-05-05 14:19

简洁

—— 来自百度百科

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=1，F(1)=1, F(n)=F(n – 1)+F(n – 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

测试环境

gcc 9.4.0 – 64位

-no-pie -std=c17 -Wall -Werror=return-type -Werror=address -Werror=sequence-point -Werror=format-security -Wextra -pedantic -Wimplicit-fallthrough -Wsequence-point -Wswitch-unreachable -Wswitch-enum -Wstringop-truncation -Wbool-compare -Wtautological-compare -Wfloat-equal -Wshadow=global -Wpointer-arith -Wpointer-compare -Wcast-align -Wcast-qual -Wwrite-strings -Wdangling-else -Wlogical-op -Wconversion -g -O0 -lm

方法一：递归

对于递归来说，一般代码相对较为简洁，但是因为套嵌调用，随着层数增加使用栈空间成指数级增加，达到一定层数后会出现栈空间不够导致段错误，另外递归时有很多重复计算（比如下面多个 f(3) ），如果计算的数据大，重复量将相当大，会消耗大量多余的时间。

int calc_fib(int num);
int calc_fib(int num)
{
    if (num < 1)
    {
        return 0;
    }
    else if (num == 1)
    {
        return 0;
    }
    else if (num == 2)
    {
        return 1;
    }
    
    return calc_fib(num-1) + calc_fib(num-2);
}

方法二 – 双指针迭代

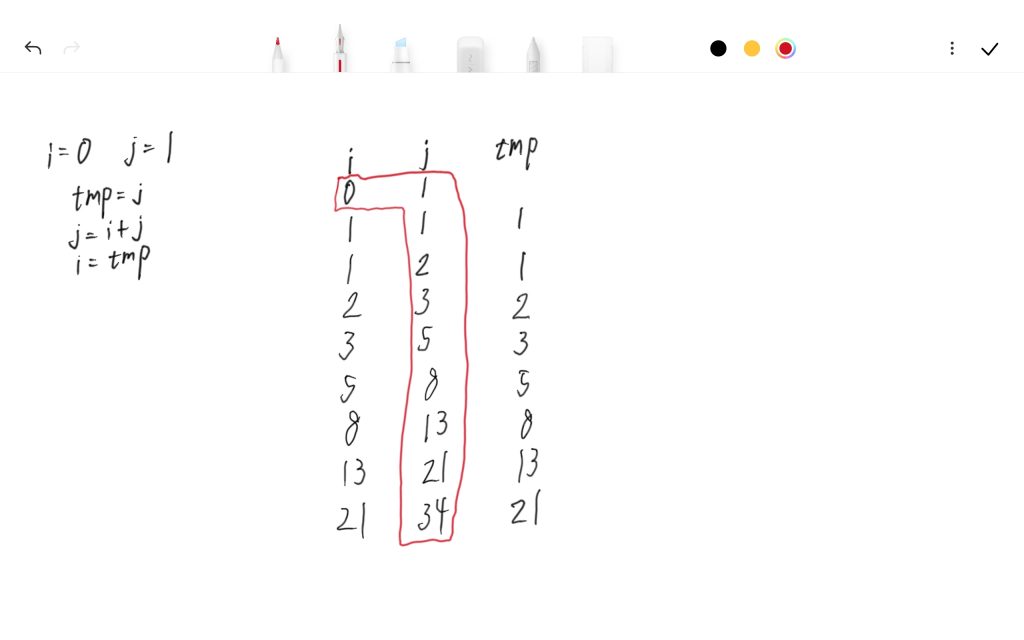
int calc_fib(int num)
{
    if (num < 1)
    {
        return 0;
    }
    else if (num == 1)
    {
        return 0;
    }
    else if (num == 2)
    {
        return 1;
    }

    int i = 0;
    int j = 1;

    for (int c = 0; c < num - 2; ++c)
    {
        int tmp = j;
        j += i;
        i = tmp;
    }
    return j;
}