排列硬币

最近更新于 2024-05-05 14:19

题目

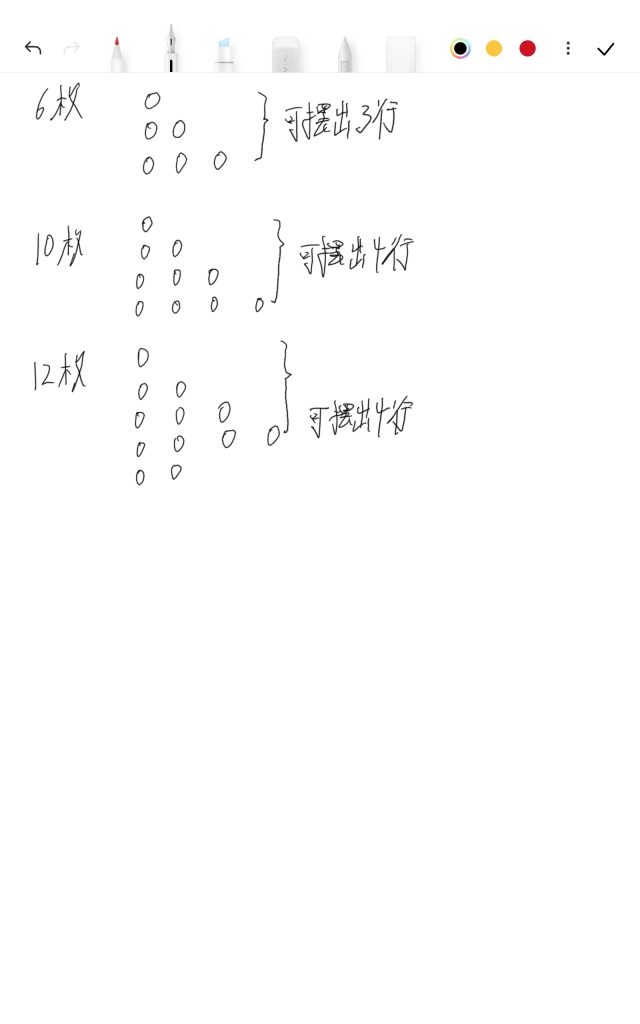
总共有 n 枚硬币，将它摆成阶梯形，第 k 行有 k 枚硬币，找出可形成完整阶梯形的总行数。

测试环境

gcc 9.4.0 – 64位

-no-pie -std=c17 -Wall -Werror=return-type -Werror=address -Werror=sequence-point -Werror=format-security -Wextra -pedantic -Wimplicit-fallthrough -Wsequence-point -Wswitch-unreachable -Wswitch-enum -Wstringop-truncation -Wbool-compare -Wtautological-compare -Wfloat-equal -Wshadow=global -Wpointer-arith -Wpointer-compare -Wcast-align -Wcast-qual -Wwrite-strings -Wdangling-else -Wlogical-op -Wconversion -g -O0 -lm

方法一：迭代

int solution(int n)
{
    int row = 0;
    while (1)
    {
        n -= row;
        ++row;
        if (n == row)
        {
            break;
        }
        else if (n < row)
        {
            --row;
            break;
        }
    }
    return row;
}

方法二：解一元二次方程

#include <math.h>


/**
 * @brief 解一元二次方程
 * 
 * @param a 
 * @param b 
 * @param c 
 * @param root 置大小为 2 的 double 数组，用于返回最终解
 */
void equation(int a, int b, int c, double root[2])
{
    int delta = b * b - 4 * a * c;
    if (delta < 0)
    {
        return ;
    }
    else if (delta == 0)
    {
        root[0] = -b / (2 * a);
        root[1] = root[0];
    }
    else
    {
        double sqrt_delta = sqrt(delta);
        root[0] = (-b + sqrt_delta) / (2 * a);
        root[1] = (-b - sqrt_delta) / (2 * a);
    }
}


/**
 * @brief 解答排列硬币问题
 * 
 * @param n 硬币总数
 * @return int 可排列的阶梯行数
 */
int solution(int n)
{
    double root[2];
    equation(1, 1, -2 * n, root);
    int i = 0;
    while (i < 2)
    {
        if (root[i] > 0)
        {
            break;
        }
        ++i;
    }
    return (int)root[i];
}

两种方法相对来说，解一元二次方程效率更高，使用迭代的话，随着要求的 fibonacci 数增大，循环的次数越来越多，而解一元二次方程是恒定的，时间复杂度为 O(1)。