最近更新于 2024-05-05 14:19
素数定义
在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数
代码测试环境
gcc 9.4.0 – 64位
编译参数:
-no-pie -std=c17 -Wall -Werror=return-type -Werror=address -Werror=sequence-point -Werror=format-security -Wextra -pedantic -Wimplicit-fallthrough -Wsequence-point -Wswitch-unreachable -Wswitch-enum -Wstringop-truncation -Wbool-compare -Wtautological-compare -Wfloat-equal -Wshadow=global -Wpointer-arith -Wpointer-compare -Wcast-align -Wcast-qual -Wwrite-strings -Wdangling-else -Wlogical-op -Wconversion -g -O0 -lm
方法一
判断某个数 N 能不能被 [2,N) 之间所有整数整除,当然也可以先行筛选掉一些明显特征的。
根据素数的特征分析出条件如下:
(1)2 是最小的素数
(2)大于 2 的素数必然不是偶数
(3)实际并不需要将 N 依次除以 [2,N) 之间的所有数,只需要除以 [2,√N] 之间的整数判断。
这个原理该怎么理解呢?
一个数 N = m × n,当 m = n 时,m=n=√N。若减小 m,那么 n 就增大,若增大 m,那么 n 就会减小,始终有 m × n = N。
如 12 ÷ 2 = 6,也有 12 ÷ 6 = 2,√12≈3.4.64。在已知 12 可以被 2 整除的情况下,对于大于 √N = 3.464 的 6 也就不需要再判断了,凡是大于 √N 的因数必然有一个小于 √N 的因数与之相乘等于 N。
#include <math.h>
#include <stdio.h>
#include <stdbool.h>
#define N 100 // 筛选素数的范围 [2,100]
int main()
{
for (int i = 2; i <= N; ++i)
{
if (i != 2 && i % 2 == 0) // 跳过偶数
{
continue;
}
bool is_prime = true;
int mid_factor = (int)sqrt(i); // 取中间因数
for (int j = 2; j <= mid_factor; ++j)
{
if (i % j == 0)
{
is_prime = false;
break;
}
}
if (is_prime == true)
{
printf("%d ", i);
}
}
printf("\n");
}

测试筛选一千万以内的素数(如果没有 printf 打印显示,速度会相当快,为了方便比较算法效率,保留 printf 可以放大时间)

方法二:埃氏筛选
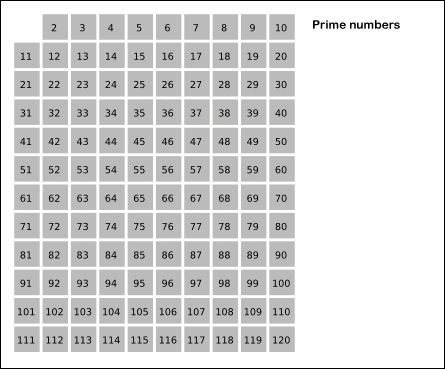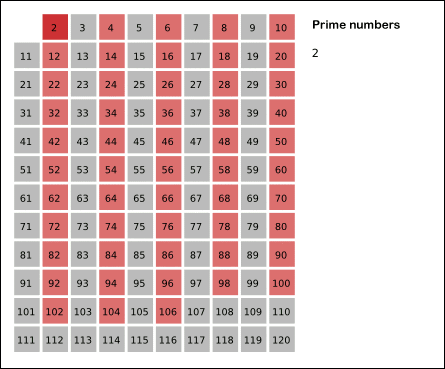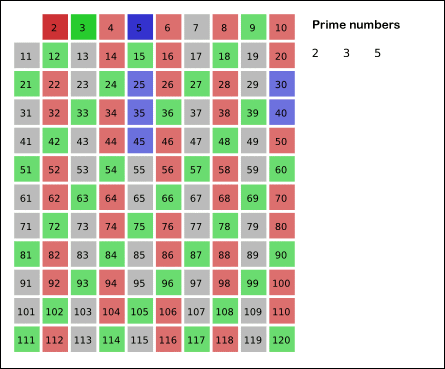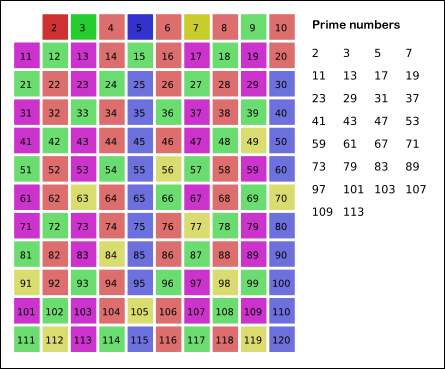
在前面我写的方法一基础上再加条件,前面是 N 依次除以 [2, √N] 之间所有整数,现在改为除以 [2,√N] 之间所有素数,进一步缩小计算量。
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <math.h>
#define N 10000000 // 筛选素数的范围
//////////////////////////////////////////////////
// 简单动态数组实现
#define INIT_LEN 10 // 初始数组容量
#define ADD_LEN 50 // 容量不够时,每次扩容量
typedef struct Array
{
int *data; // 存放数据
size_t size; // 数据实际长度
size_t capacity; // 容量
} Array;
/**
* @brief 创建一个动态数组对象
*
* @return Array* 返回创建的对象
*/
Array *create_array()
{
Array *new_array = malloc(sizeof(Array));
int *new_data = malloc(sizeof(int) * INIT_LEN);
new_array->data = new_data;
new_array->size = 0;
new_array->capacity = INIT_LEN;
return new_array;
}
/**
* @brief 向数组中添加元素
*
* @param array 要添加元素的数组对象
* @param val 要添加的值
*/
void add(Array *array, int val)
{
if (array->size + 1 > array->capacity) //扩容
{
array->data = realloc(array->data, sizeof(int) * (array->capacity + ADD_LEN));
array->capacity += ADD_LEN;
}
array->data[array->size] = val;
++array->size;
}
/**
* @brief 下标索引数组元素值
*
* @param array 要索引的数组对象
* @param idx 下标值
* @return int 索引结果
*/
int get(Array *array, size_t idx)
{
if (idx >= array->size)
{
return -1;
}
return array->data[idx];
}
/**
* @brief 返回数组长度
*
* @param array 要获取长度的数组对象
* @return size_t 数组长度
*/
size_t len(Array *array)
{
return array->size;
}
/**
* @brief 释放数组(结束时必须调用该函数释放数组占用的内存)
*
* @param array 要释放的数组对象
*/
void free_array(Array *array)
{
free(array->data);
array->data = NULL;
free(array);
array = NULL;
}
// 简单动态数组实现
//////////////////////////////////////////////////
int main()
{
Array *prime = create_array(); // 用于存放素数
add(prime, 2);
for (int i = 3; i <= N; i = i + 2) // 遍历筛选范围内的数 - 偶数直接排除
{
bool is_prime = true;
int mid_factor = (int)sqrt(i); // 计算边界 √N,N 除以所有 [2,√N] 之间的素数
size_t length = len(prime); // 已有的素数个数
for (size_t j = 0; j < length; ++j)
{
int div = get(prime, j);
if (div > mid_factor)
{
break;
}
if (i % div == 0)
{
is_prime = false;
break;
}
}
if (is_prime == true)
{
add(prime, i);
}
}
for (size_t i = 0; i < len(prime); ++i)
{
printf("%d ", get(prime, i));
}
printf("\n");
free_array(prime);
}
下面就是直接测试筛选一千万以内的素数,耗用的时间接近前一种方法的一半
素数筛选
