椭圆

标准方程： $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

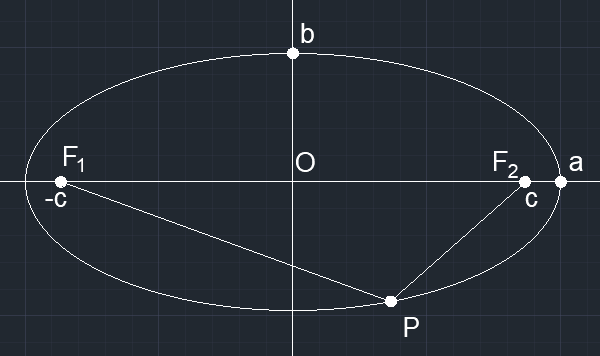
a 为长半轴，b 为短半轴，c 为焦点，三者关系： $a^2=b^2+c^2$
P 为椭圆曲线上一点，则有 $|PF_1|+|PF_2|=2a$
离心率： $e=\frac{c}{a}$ （接近 0 就圆，接近 1 就越扁）

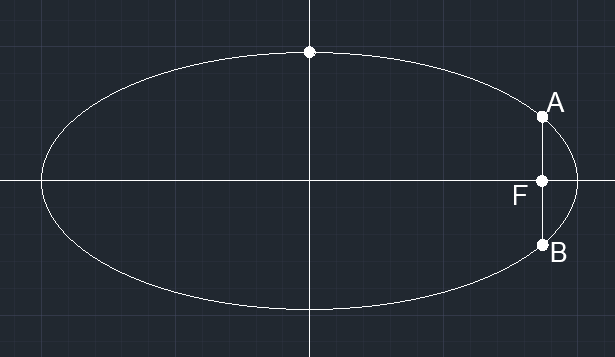
通径： $|AB|=\frac{2b^2}{a}$

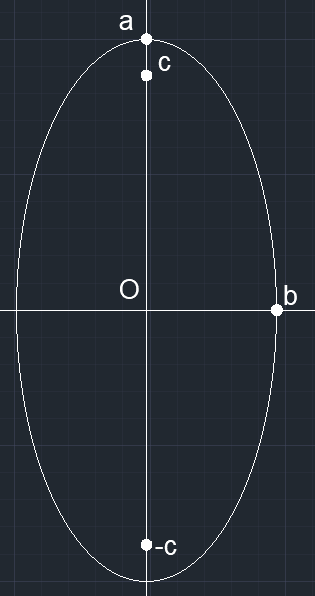
长轴在 y 轴的话方程就是： $\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$

双曲线

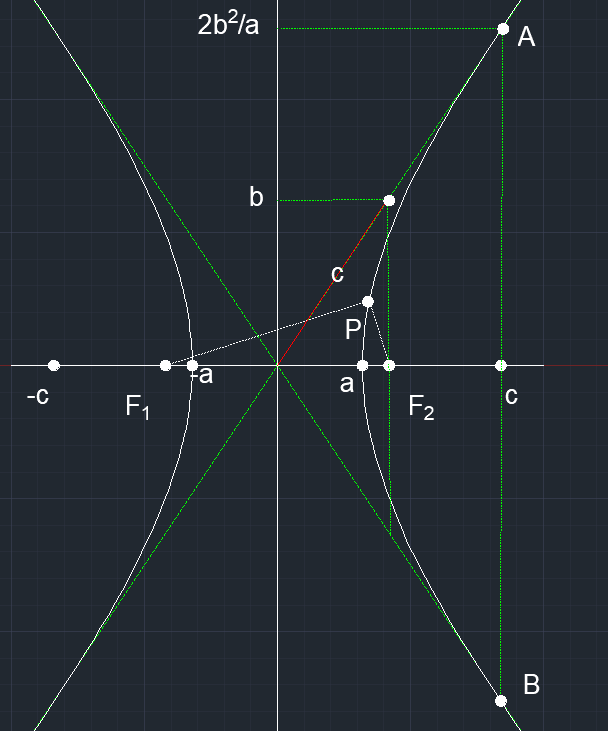
标准方程： $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$
如果是关于 x 轴对称的双曲线，则是 $\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$

两个顶点间长度为实轴长，即 2a，过顶点与实轴垂直交于两条渐近线的两点，这两点间为虚轴长，即 2b，则原点到其中一个交点的距离即为 c。三者关系为 $c^2=a^2+b^2$
P 为双曲线上一点，则有 $||PF_1|-|PF_2||=2a$
两条渐近线方程（过原点的两条绿色虚线）： $y=\pm\frac{b}{a}x$
离心率： $e=\frac{c}{a}$
通径： $|AB|=\frac{2b^2}{a}$

抛物线

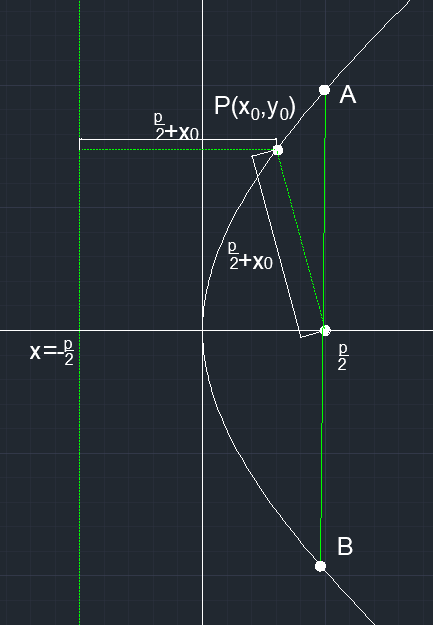
标准方程： $y^2=2px$ （ $p\gt0$ 时，图像在正半轴， $p\lt0$ 时，在负半轴）
如果抛物线在 x 轴上侧或下侧，则方程 x 和 y 对换位置即可

抛物线的离心率恒为 1
a 为焦点 $(\frac{p}{2},0)$ 到准线( $x=-\frac{p}{2}$ )距离的一半，即 $a=\frac{p}{2}$ ；b 为抛物线顶点横坐标，即 0；c 为焦点到顶点的距离
通径：|AB|=2p

圆锥曲线